はじめに
本校は,令和４年度より数理データサイエンス科を新設し,データサイエンティストの素養をはぐくむことを目的としたカリキュラムのもと,関連する資質・能力の向上を図っている。特に数学科においては,データサイエンスを学ぶ上で重要な土台となる統計の指導を担っており,これらを担保するためにＳＳＨのカリキュラムマネジメントの枠を利用して,「ＳＳ統計学」を学校設定科目として設定した。この科目の具体的な内容を以下に紹介したい。
目的
「ＳＳ統計学」は,数理データサイエンス科２年次で履修する「理数数学Ⅱ」の６単位のうち,ＳＳＨ科目として１単位を分離する形で設定した学校設定科目である。本科目は,学習指導要領でも重要性が謳われている数学Ｂにおける推測統計の内容を,課題研究で活用できるようなレベルで学習するという内容となっている。数学Ｂで学習する内容に加えて,データの抽出方法（系統抽出法,層別抽出法,多段抽出法）および推定と検定（Ｚ分布,
分布，Ｆ分布，
分布，ノンパラメトリック）まで学習を行うとともに，それらを課題研究の中で活用していく事をねらっており，その主な目的は以下の通りである。
| ① 記述統計および推測統計における知識・技能を課題研究で活用できる視点で身に付ける。 ② 統計的な処理の結果に基づいて，問題 の特性を捉えた適切な考察ができるようにする。 ③ 統計の知識・技能を課題研究等の問題解決に積極的に利用しようとする姿勢を養う。 |
生徒の学習環境
生徒は学校を通して一人一台Chromebookを購入し,所持している。このタブレットは授業中自由に使用することができ,「SS統計学」の授業においては,Google Driveを用いた教材の配付に利用している。統計の演習には,Spreadsheetを用いて必要な統計量や関数を自分で入力できる教材を準備し,生徒が授業時間外でも内容を振り返ることができるようにしている。また,学校のウェブサイトを通じて,「ＳＳ統計学」の授業内容の簡易版をオンデマンドで配信しているため,生徒は課題研究に取り組む際など,さまざまな場面を通じて授業の内容にアクセスすることができる。このようにＩＣＴを活用して必要な環境を整えることで,生徒の自発的な統計の活用を促している。
学校のウェブサイトオンデマンド配信へのリンク
（https://www23.sapporo-c.ed.jp/asahigaoka/index.cfm/1,12910,46,html）
実施内容
| 大単元 | ねらい | 学習内容 |
| 標本調査法 | データ収集の際に用いる標本抽出において，母集団の状況に応じた信頼度の高い方法を選択する。 | 復元抽出と非復元抽出，単純無作為抽出法 多段抽出法，層化抽出法，系統抽出法 |
| 統計的 仮説検定 |
データの分析に欠かせない統計的仮説検定の方法について知るとともに，それらを具体的な状況に適用できるようにする。扱う検定の内容を下記の通りとする。 ・正規分布に基づくパラメトリック検定およびノンパラメトリック検定を区別できる。 ・パラメトリック検定において，用いる検定を決定する要素として，データ数，平均値，分散が大きな役割を果たすことを理解する。 ・複数の標本間の検定において，データの対応の有無が重要な要素となることを理解する。 |
正規分布と大数の法則，中心極限定理, 有意水準, 棄却域, Ｚ検定の方法，危険率及び過誤，両側検定と片側検定，分布と分布表，検定の方法, 標準正規分布表, Ｆ分布とＦ分布表，Ｆ検定の方法，Ｆ検定における左側検定，対応のあるデータと対応のないデータ，等分散性の判断,スチューデントの検定とウェルチの検定，分布と分布表，検定における左側検定，分割表，適合度の検定，コルモゴロフ・スミルノフ検定，イエーツの補正，独立性の検定，ｍ×ｎ分割表，対応のない２群間の検定，マン・ホイットニーのＵ検定, ＱＱプロット |
| 統計的推定 | 統計的推定と統計的仮説検定の違いについて理解する。 ・点推定と区間推定の違いについて理解する。 ・信頼度の意味について理解する。 |
統計的推定とは，点推定と区間推定，信頼区間 信頼度，信頼区間の求め方（95%・99%） 回帰係数における推定・検定， 母回帰係数の信頼区間 |
| 回帰分析 | 回帰の意味およびその手法について理解をし，回帰に基づく現象を数学のモデルとして表すことのよさを知り，主体的に回帰分析を利用しようとする態度をはぐくむ。 ・単回帰分析と重回帰分析の違いやそれぞれの手法について理解し，具体的な事象について回帰分析ができるようにする。 |
単回帰と重回帰の違い，単回帰分析の活用場面 説明変数と目的変数，回帰直線，最小二乗法，内挿と外挿，決定係数，回帰係数における推定・検定，ピアソンの相関係数におけるｔ検定 母相関係数の比較値との差のｚ検定，スピアマンの相関係数，重回帰の意味，重回帰式，偏回帰係数，相関係数行列，回帰推定値と残差，重回帰の分散分析と重相関係数，寄与率と重相関係数，重相関係数の有意差検定，偏相関係数 |
| 実験計画法 と分散分析 |
複数の群における検定の方法について理解するとともに，結果の考察の仕方について知る。 ・二元以上の実験データから効率よくサンプルを選択する方法を知る。 ・多変量データにおいても基本となる検定の考え方は変わらないことを知る。 |
実験計画とは，一元配置法，二元配置法，乱塊法，ラテン方格法，交互作用，直交表，線点図，実験データのサンプルを用いた分散分析の演習，ランダム化と層別，因子数と実験の繰返し, 多重比較, Bonferroni法, Tukey-Kramer法, FWER |
授業の内容
これまでの数学Ｂにおける推測統計の学習は，理論や計算に終始してしまい現実の場面で活用することは皆無に等しく，統計の有用性について理解する機会や統計の知識・技能を課題研究をはじめとする身の回りの様々な場面に用いようとする意欲がうまくはぐくめていなかった。統計の知識・技能は，現実の曖昧な事象に対しても第４のパラダイムと呼ばれる科学的な根拠となり，それらをうまく活用することが自らの主張の正当性を高めることを生徒に実感させることが重要である。本授業を通じて，生徒に多様な統計処理の方法や用いるべき状況や条件を把握させるとともに，積極的に統計の知識・技能を活用しようとする意識をはぐくむことを目標に毎時間の授業を構成している。
【授業の実際（適合度の検定の例）】
① 統計の知識・技能について具体的な事例を通して，統計処理の方法を理解する。
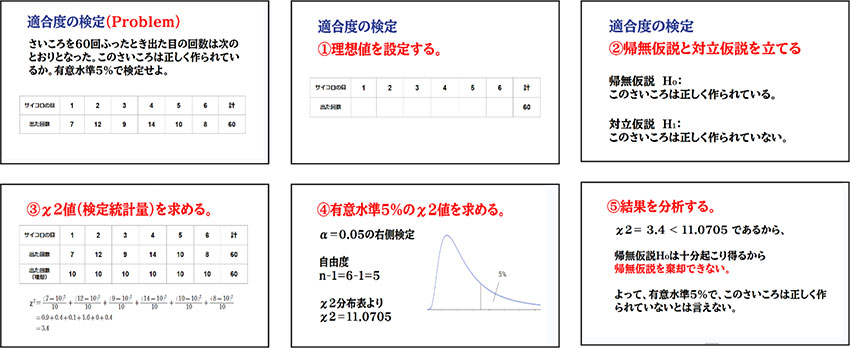
上記のようなスライドを準備して，それぞれの統計についての処理の方法及び，具体的に用いる場面や状況について教員に説明を受ける。
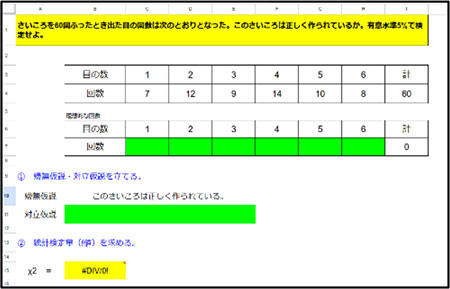
② Spread Sheetを用いて，生徒が自力で例題の検定を行う。
Spread Sheetの緑色のセルに自分自身で数値や用語を入力し，統計処理の一連の方法を把握しやすいようにした。複雑な検定統計量の計算は，関数で自動的に導出されるようにし，全体的な統計処理の流れや，検定の結果からどのような判断ができるのかどうかを考察することに時間を掛けられるようにしている。検定に必要な分布表は，別シートで参照できるようにし，極力教員の力を借りずに自分自身で統計の処理ができるように工夫をしている。
③ 類題に挑戦をする。
類題を用意し，自分の理解度に合わせて授業時間内で検定の処理を進める。今回の例で用いた適合度の検定に関しては，以下の類題を準備した。類題は毎回３,４問準備し，少しずつ処理の難易度をあげていく構成となっている。このように統計の知識を必要に応じて少しずつ発展・補完していくことが生徒の統計活用能力を高めていくことに繋がると考えている。
A町の1年間で起きた交通事故件数は，曜日別にまとめると以下のようになった。このとき，交通事故は特定の曜日に起こっていると言えるだろうか。
ある幼稚園で，30人の園児に，A，B，Cの3種類のおやつのうちどれが一番好きかを聞いたところ，8人がAを，17人がBを，5人がCを選んだ。この結果から，園児は特定のおやつを好む傾向にあるかどうかを，有意水準0.05で検定すること。
上記①～③の構成で，毎時間の授業を進めることで生徒に少しずつ統計の活用における素養を高めていった。このように学習を進めることにより，生徒に課題研究や日常の学習の中で徐々に統計用語や検定を実際に用いようとする姿勢が見られるようになってきており，取組の効果が見られる。本授業後，生徒が統計を活用する意欲を向上させる目的で，授業内で適合度の検定を用いた数時間の探究に取り組ませた。下記に生徒の発表スライド（抜粋）を掲載する。
【適合度の検定を用いた探究】
探究の発表をする上で，以下の点に留意させた。
- 検定の流れが見えること。特に，理想値をどのように設定したかについてしっかりと説明すること。
- 結果の考察について，仮説の採択に関する記述のみからは見えない視点を含め，できる限り次の問いに繋がるような考察を行うこと。
- 探究の過程において統計の誤用等の失敗があった場合，それらを振り返り全体に共有すること。統計の活用においては，状況に応じた様々な見方や考え方が必要になるためそれらを共有し，全体で高めていくことは重要である。
おわりに
このような学びを経験することで，生徒は課題研究において積極的に統計を活用しようとする態度が高まっており，それらは生徒が統計の用語をよく話題にしていることや教員に統計の知識や利用に関して質問をしてくることからも見取ることができる。課題研究で利用頻度の高い多変量解析などの高度な統計の手法を生徒が自発的に活用していくことは，この科目を設定した大きな目的でもあるため。今後，生徒の統計の素養をさらに高め，社会で活用できる人材の育成に励みたい。