

本単元の内容は「異種の量の割合」と言われる。一方に「同種の量の割合」があり,これがいわゆる教科書の「割合」である。子どもにとって大きな壁である「割合」の学習だが,本単元の学習内容は割合に特に関わりが強く,前段階のステップと考えたい。
子どもたちにとって本単元で学習する量は,これまで学習してきた長さ,かさ,重さ,面積などの量とは全く異なる。それは,これまで学習してきた量が,規準のいくつ分かで比べられるのに対し,本単元で学習する量は規準のいくつ分かで比べることができないからである(外延量と内包量)。人数だけで混み具合が比べられないように,本単元では,①一つの量では比べられない事象があることに着目する。そして,②その事象を比べる方法や,数値化する方法を考える。例えば,「人数」と「広さ」の関係で混み具合を比べようと考えることである。
さらに,③計算して求められた数値が何を表すのかを捉えることも大切である。例えば,700kmを35Lのガソリンで走る車に関して,700÷35=20と計算し,その20は何を表しているのかを考えることである。20が何を示すのかが分からなければ,他方と燃費性能を比べることはできない。また,35÷700=0.05と計算して比べることも可能であるが,20と0.05の関係をつかむこともできない。
上の①~③を意識しつつ学習を進めても,理解に困難さを示す子どもにたくさん出合ってきた。そうした子どもたちとよくよく話をしていると,上記の3点以前の段階に違和感をもっていることが見えてきた。割合の学習までを見越すと,本単元の導入には少し時間をかけて,子どもが感じる違和感を引き出し,越えておく必要があると感じた。以下に導入のポイントを示す。
「混んでいる」とはどういうことか,子どもの経験はそれぞれに異なる。渋滞を「混む」と言うことが多いが,それ以外の「混む」に出合っていない子どもにとっては,「どちらが混んでいますか」という問いはそれ自体がハードルとなる。これは例えば,「どちらが揺蕩(たゆた)っていますか」と問われた私たち大人の状況とよく似ているのではないだろうか。そこで,単元の最初はまず,「混んでいるとはどんなとき」と問うことから始める。極端な例の写真などを示し,2つの状況を比べるというのも有効である。
例えば,下のような2つの状況を見て,クラスの子どもは混み具合をどのように判断するだろうか。

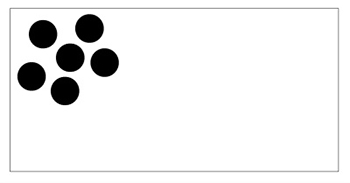
右の方が混んでいると判断する子どもは少なくない。どちらも同じだと考えるためには,右の●を動かして●1つ分に対する広さを均等にしなければならない。ここに平均の学習が関連してくる。子どもの言葉をもとにして,均等にして考えるべきだと確認したい場面である。なお,この●は,人や動物などの動く物だという文脈が大事である。木や花などは散らばりを均等にするイメージはもちにくい。
「10畳の部屋に6人」と,「9畳の部屋に5人」の混み具合を考えたとき,10-6=4と9-5=4でどちらも4だから混み具合が同じだとする考え方がある。この4は,1人が1畳使った時に余る畳の数であり,余った広さが同じだから混み具合が同じだとする考えである。図的に説明しても納得度は高い。実は,子どもがこれまでに学習してきた比べ方は2つの差で比べる方法であり,むしろ自然な考え方だと言える。差で比べてもいいと考える子どもにとって,割り算をする必要性はない。数値の設定によってこの考えの出やすさは異なるが,経験上,必ずこの考えは出てくる。数値を工夫して,あえて差で比べる考えが出るようにし,差で比べる考えを正面から越えることが,子どもがもつ違和感を減らすと考える。
数値の設定は,広さよりも人数の方が少ないことが好ましい。例えば「5枚のマットに28人」といった状況では,1人1枚にすると23人が余るというアイデアは出にくい。また,差で比べた時と,割合で比べた時の混み具合の判断が異なることが必要である。例えば「A:10枚に6人」と「B:8枚に5人」では,差で比べた結果と,割合で比べた結果がどちらもBの方が混んでいるという判断になる。これでは,「どっちも結果が同じだから,どちらでもいい」と差で比べる考えを発展させる必要性がなくなる。
| 広さ | 人数 | 差の考え | 単位量あたりの考え |
| 10枚 | 6人 | 10-6=4 | 10÷6=1.666… |
| 8枚 | 5人 | 8-5=3 (混んでいる) | 8÷5=1.6 (混んでいる) |
一方,「A:10枚に6人」と「B:9枚に5人」では,差で比べると「混み具合が同じ」となり,割合で比べると「Bの方が混んでいる」となる。
| 広さ | 人数 | 差の考え | 単位量あたりの考え |
| 10枚 | 6人 | 10-6=4 (同じ) | 10÷6=1.666… |
| 9枚 | 5人 | 9-5=4 (同じ) | 9÷5=1.8 (混んでいる) |
ここで,考えを「発展させる」としているのは,差の考え方をもとにして,割合の考え方に変容させることができるからである。具体的には,余った畳を再配分すること。そして極端な例を示すことである。詳しくは実践にて紹介する。
混み具合を比べる考えには,一方を公倍数でそろえて比べる考え方もある。例えば,「10畳の部屋に6人」と,「9畳の部屋に5人」を比べる時に,畳の数を90枚にそろえる考えである。6人×9=54人と,5人×10=50人だから,54人になる部屋が混んでいると考える。この考えには,「部屋と人数の両方が10倍になれば混み具合は変わらない」という比例の関係をつかんでおくことが必要となる。
比例に基づいて考えているため,これは割合で比べる考えと結果が同じになる。そして,1あたりで比べるよりも,公倍数にそろえて考える方が分かりやすいという子どもはかなり多い。これも,正面から越える場に出合わせたい。具体的には,公倍数が出しにくい新たな部屋を提示したり,複数の部屋の混み具合を順位付けしたりする課題を設定する。2つの考えが似ていることを確認した上で,2つの方法の違いがわかる課題を設定したい。
ここまで述べたポイントを整理すると,以下の7点になる。
①一つの量では比べられない事象があることに着目する
②事象を比べる方法や,数値化する方法を考える
③計算して求められた数値が何を表すのかを捉える
(1)「混んでいる」生活経験を引き出す
(2)均等にして考えることを確認する
(3)差で比べる考えを発展させる
(4)公倍数の考えよりも単位量あたりの考えが便利なことを経験させる
本実践として,単元の最初の3時間を紹介する。
まずは「混んでいるとはどんなとき」と問うことから始めた。子どもからは,「高速道路の渋滞,エレベーター,満員電車,デパートのセール」などが出てきた。そこからは,「ぎゅうぎゅう」「せまいところ」「人がたくさん」などの表現が出され,「混む」ということを共有することができた。
次に2つの図を示した。

図ア

図イ
子どものつぶやきから人数と広さが等しいことを確認した。続いて,どちらが混んでいるかを問うた。ほとんどの子どもが図イの方が混んでいると判断した。少数であった図アの方が混んでいると判断した子どもに理由を問うと,「図アと図イの人数が同じで近くに集まっているだけだから」「広がったら同じ」と発言した。教師が図イに矢印を書き加え,「こういう感じ?」と確認すると,これを聞いた多くの子どもは混み具合が同じという考えに納得したようであった。そこで1人が,「人で考えたらイが混んでるけど,部屋で考えたら同じ」と発言した。これをもとに,混み具合は「部屋で考える」こと,つまり散らばりを均等化して,平均で考えることを確認した。
最後には右の図ウを提示し,3つの部屋の混み具合を比べるよう発問した。人数は3つとも等しいが,図ウは図ア・イに比べて部屋が狭いように見える。「人数が同じだから狭いウの部屋の方が混んでいる」という発言を全員が受け入れ,混み具合は,人数と部屋の広さで決めることを約束した。

図ウ
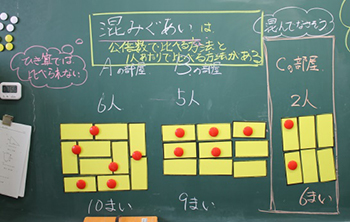
まず2つの部屋の混み具合を比べることを伝え,人数だけを示した。Aの部屋が6人,Bの部屋が5人である。「どっちが混んでいますか」と問うと,「広さによる」「もし広さが同じならA」という反応がすぐに返ってきた。そこで,この部屋が和室だという設定を伝え,図で2つの部屋の広さを示した。
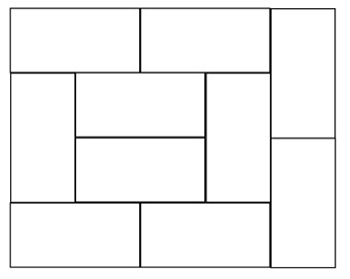
Aの部屋
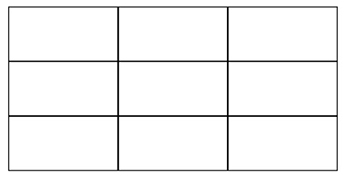
Bの部屋
この図から,Aが10畳,Bが9畳だと確認したところで,1人の子どもが手を挙げた。
T:何か質問?
C:質問じゃないけど…混み具合は一緒?
T:混み具合は一緒。それは頭の中で何か計算したの?
C:してない。Aは6人で10枚で,5人が1人少なくて…
T:ああ,なるほど,もう考え始めてるんだね。ぜひそれを書いてほしい。それでは少し考える時間をとります。
差の考えにつながる発言のようであったが,ここではこの発言を共有することは避け,自由に考える時間をとった。
机間指導している間には,興味深いやりとりが聞こえてきた。「6人って言っても,お相撲さんだったり,子どもだったり,細い人だったりいろいろおるやん?だから,部屋にいる人がどんな人か言ってくれないとわからない。」「もし6人が全員大きくて,5人が全員小さかったら…」これを聞いて,教師は「力士ならせまいけど」と板書した。その後は,それぞれに体格が関係するかどうかを議論していた。
C:人数なんやから体格とか関係なくない?
C:でもきゅうきゅうなことを混み具合って言うんやから…人の体格によってはきゅうきゅうになるんちゃう?がい骨ならきゅうきゅうじゃなくなるよな。
また,部屋の形の違いを気にする子どももいた。Aの方が正方形に近く,Bは長辺と短辺の差が大きい。その子は畳10枚をなんとか長方形にしようと並べ方を模索していた。
自分で考えをもち,少人数で交流した後,全体で考えを交流した。全体の交流では6つの考えが出された。

差で比べる考えがHである。ここからの考えの共有は導入の図にマグネットを重ね,操作させながら行った。Rはそれに続ける形で,余った4枚をさらに分けることを考えた。その分け方は1人に1枚ずつ分けるもので,2枚目の畳を割り当てられない人数を計算した。Aの部屋は6人-4枚=2人がもらえない。Bの部屋は5人-4枚=1人がもらえないという考えである。余った4枚を等分する考えでないため,まだ差で比べる考え方であるが,余った分を再配分するというアイデアは割合の考えにつながる発展途上のものだと言える。
Sの考えは,演算の意味や,計算結果の数値が何を示すかを捉えきれていない典型のものであった。
S:Aの6人が,Bの畳9枚に入ってると考えて,これ(Aの6人)とこれ(Bの枚数)をまずかける。6×9。
C:ん?
S:で,答えが54になるけど,その答えは…また違うものと考えて。
C:違う物
S:54は畳の枚数。
C:ん?畳の枚数っておかしくない?
T:まぁ,最後まで聞こう。
S:で,その54を6でわって9。
C:6かけて,6でわったら意味ないと思う。
T:意味ないとか言うなよ。Sはこの9を何だと思ったの?
S:…
T:ちょっと考え中?
たすのか,ひくのか,かけるのか,わるのか,どれだろうと考えることをスタートにする子どもは少なくない。Sは自力解決の中で,あらゆる演算をびっしりノートに書いていた。たしたものをひいたり,かけたものをわったりなどである。自分なりに試行錯誤を繰り返した姿勢を価値づけた上で,どちらが混んでいるかは判断がつかないことを確認した。
Kは畳1枚に2人を配置し,余った広さで比べるアイデアであった。差で比べる考えであるが,「畳1枚に2人くらい入るかなと思って…」という,より具体的にイメージした考えであった。この時点で,「Aが混んでいる」「混み具合は同じ」「Bが混んでいる」という3つの考えが出ることになった。
YとMの考えは畳の数を公倍数でそろえる考えであった。どちらの部屋も畳90枚にそろえるというYの考えは,友だちに受け入れられないようであったが,「通分と似てる」という子どもの発言で多くの子どもがその意味をつかんだようであった。Mはその考えを公倍数という言葉で意味づけた。
最後はWの割合の考えであった。1人あたりの畳がAの部屋は1.666…枚,Bの部屋は1.8枚となることを説明した。これらの考えの混み具合の判断がそれぞれに異なることから,次の時間に考えることを整理して第2時を終えた。
第2時の板書をそのまま残しておき,第3時へと入った。まず前時を振り返って,今,自分の中でどれが最も有力な考え方かを問うことから始めた。その結果,表のような結果となった。S自身もRの考えに変わっていた。
次に,「今の時点で同じ考えをもった人と近くに集まりましょう」と指示した。続いて,新たな部屋Cを提示した。Cは6畳に2人である。
| H | 5人 |
| R | 25人 |
| S | 0人 |
| K | 4人 |
| Y&M | 2人 |
| W | 1人 |
提示した段階で,広々と感じることなどの声を期待したが,この時には反応は薄かった。ここで教師は,「今のあなたの考えで,Cの混み具合を考えるならどうなりますか」と発問し,それぞれに考える時間とした。
その後,全体の交流に入る段階で,感覚的に混んでないのはどれかを確認しておくこととした。
T:ちなみに,考えを聞く前に,一番広々としてそうなのはどれ?
C:Cの部屋(多数)
T:自分Cの部屋やったら広々とできそう?
C:Cの部屋に住みたい
T:広々としているってことは,混んでないってことだよね?
Cの部屋はいちばん混んでないってことはみんな賛成かな?
C:OK!
Cの部屋が最も混んでいないという感覚と,計算方法の結果が同じになるかどうかを焦点とした。
全体の交流では,まず公倍数で比べるYの考えから確認し,続いてK,H,W,Rと進めていった。それぞれに図と式とを関連づけながら,計算で求められる数値が何を示すのか,その数値の大小が混み具合の判断にどうかかわるのかを丁寧に確認することを大事にした。それぞれの結果を表にまとめると下のようになる。
| 考え方 | A(10畳6人) | B(9畳5人) | C(6畳2人) | Cの混み具合 |
|---|---|---|---|---|
| H(差:1人1枚) | 4枚あまる | 4枚あまる | 4枚あまる | A・Bと同じ |
| R(差:発展途上) | 2人が2枚目を もらえない |
1人が2枚目を もらえない |
むしろ3枚目まで もらえる |
最も混んでいない |
| K(差:2人1枚) | 7枚あまる | 6.5枚あまる | 5枚あまる | 最も混んでいる |
| Y(公倍数) | 90畳に54人 | 90畳に50人 | 90畳に30人 | 最も混んでいない |
| W(1人あたり畳) | 1.666…枚 | 1.8枚 | 3枚 | 最も混んでいない |
このように確認すると,Cの部屋が最も混んでいないという感覚と合致するのはR,Y,Wの3つとなる。そこで,Rの「余った分をさらに配る」というアイデアについてさらに話し合うことにした。
T:Rの考えでいくと,Bの部屋で2枚目をもらえなかった1人はかわいそうだね。どうにか平等に分けられないかな?
C:ちょっと余るところもあると思うから,隣の人のところをちょっと貸してもらう。
T:なるほど,こうやって2人で3枚使う感じ?
C:だったら余りを全部5人で分ければいい。
T:ほう。それ計算としてはどうなる?
C:5÷4
C:4÷5
C:4枚を5人で分けるから,4÷5。
T:どう?じゃあ4÷5を計算してみよう。
・・・・
T:どうなった?
C:0.8
C:ということは,結局一緒だ。
T:どういうこと?
C:考え方がちょっと違うだけで,答えは一緒だから,Wと一緒。
T:Wと一緒。気持ち分かる人?
C:Wの方も,Bの部屋の9枚あるものをケンカにならないように5人で分けようと考えてて,9÷5の1.8っていうのは,1人が使える畳の枚数。で,今計算したのは,余ったのをケンカしないように分けて0.8で,1人1枚と0.8枚でどちらも同じ事になる。
余った畳を等分してみることで,0.8枚という数が導かれた。等分しようとした場合は1人あたりの枚数で比べることと同じになることが確認された。子どもたちの反応も「あぁ,なるほど」と納得が得られたような大きな反応であった。余った畳をさらに分けようとしたアイデアを価値付け,公倍数でそろえるYの考えと,1人あたりで比べるWの考えの2つが残る状態となった。

ここで,「混み具合は一方を公倍数でそろえて比べる方法と,1あたりで比べる方法がある」と結論づけた。その上で,練習問題を新たに提示した。「92㎡に69人」と「70㎡に56人」との混み具合を比べる問題である。個人で考える時間をとった後,公倍数(Y)と1あたり(W)のどちらの考え方で比べたかを聞くと,全員が1あたり(W)で比べる方法であった。理由は,「公倍数が大きすぎる」というものであった。ここで,どんな数字でも,いつでも使いやすいのは公倍数の考えよりも,1あたりで考えることだということを確認した。
1あたりで比べる考えには,1人あたりで比べるものと,新たに1㎡で比べるものとが出てきた。これらの数値の大小関係と,混み具合の判断は,次時の燃費の問題につなげることとした。
本単元の学習を難しいと感じる子どもの違和感をできるだけ減らすことを目的として,導入段階で子どもの感覚を引き出し,1つずつ乗り越えることを大事にした。
特に,2で挙げた4つの項目,(1)「混んでいる」生活経験を引き出す。(2)均等にして考えることを確認する。(3)差で比べる考えを発展させる。(4)公倍数の考えよりも単位量あたりの考えが便利なことを経験させる。これらはかなり有益に働いたと考える。算数科の積み上げの中では「できている」とされることでも,実際には1つずつ確認していく丁寧さが必要なのかもしれない。
新たな発見だったのは,第2時であった。「人の体格によって混み具合がかわる」「部屋の形をそろえる必要がある」という子どもの感覚には納得させられた。もしかしたら,これまで教えてきた子どもたちの中にも,口には出さないがそうした違和感を感じていた子どもがいたかもしれない。素直に表現してくれた子どもたちに感謝したい。
本実践を経て,単位量あたりの大きさ,割合の学習へと入ったが,全員が完全に理解できるという状況は作れなかった。それでも自分なりの考えをもって授業に参加できる子どもを増やすことができたのではないかと感じている。今後も子どものわからなさに寄り添う努力を続けていきたい。