

漸化式の解き方は教科書が与えているものより簡単な方法があることは,教員になってから学ぶことになりました。多項間漸化式へのいくつかのアプローチを例に挙げながら,高校生は受験に向かって,教員も数列について授業するとき,定期考査を作るとき,知っていて損はないと思える内容を共有できたらと思います。
【問題1】※千葉大学 2015年
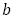 と
と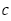 を
を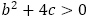 を満たす実数として,
を満たす実数として,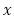 に関する2次方程式
に関する2次方程式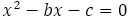 の相異なる解を
の相異なる解を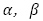 とする。
とする。
数列 を
を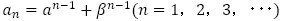 により定める。このとき,次の問に答えよ。
により定める。このとき,次の問に答えよ。
(1)数列 は漸化式
は漸化式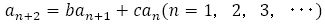 を満たすことを示せ。(2)略
を満たすことを示せ。(2)略
【問題1】について証明は代入して確認するだけで,難しいものではありません。特に,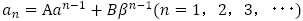 と係数が1でなくとも同様に漸化式を満たします。このことを利用して,次の【問題2】を処理します。これは有名な方法であると思いますが,念のため確認しておきます。
と係数が1でなくとも同様に漸化式を満たします。このことを利用して,次の【問題2】を処理します。これは有名な方法であると思いますが,念のため確認しておきます。
【問題2】
次の条件によって定められる数列 の一般項を求めよ。
の一般項を求めよ。
(1)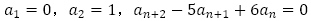
(2)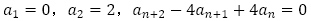
(1)について,特性方程式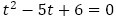 から解
から解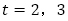 を得て,数列
を得て,数列 の一般項を
の一般項を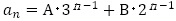 とおき,
とおき,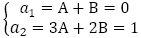 を解き,
を解き,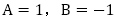 を得ることで,
を得ることで,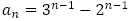 と求めることができます。
と求めることができます。
教科書らしい式変形を施しながら解く方法に比べて,格段に早く処理できるので,高校生でも知っていて損がないと思います。この解法により得た解が,必要十分であるか,生徒が答案に記述した場合どのような扱いとすべきかについては今回の記事では言及しないこととします。
(2)について,特性方程式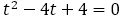 から重解
から重解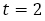 を得て,数列
を得て,数列 の一般項を
の一般項を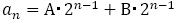 とおくのではなく,
とおくのではなく,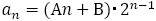 とおくことに注意が必要です。【問題1】では,この問題を解消するために
とおくことに注意が必要です。【問題1】では,この問題を解消するために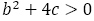 としてあります。一般項の形を決めた後,
としてあります。一般項の形を決めた後,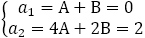 を解き,
を解き,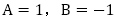 を得ることで,
を得ることで,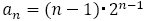 と求めることができます。
と求めることができます。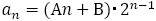 が漸化式を満たすことは簡単に確認できます。
が漸化式を満たすことは簡単に確認できます。
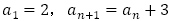
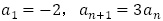
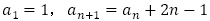
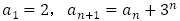
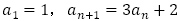
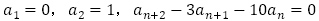
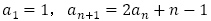 (取り扱っていない場合が多い)
(取り扱っていない場合が多い)【問題3】は,(2),(6)と(1),(3),(4),(5),(7)に分類できると考えます。最も簡単な例として,(1),(2)を扱うのは良いと思いますが,階差数列を利用する(3),(4)は生徒にとって理解の良いものではないように思えます。体系的に漸化式を扱うのであれば(5),(6)とは切り離して扱わない方がよいだろうと思います。この記事において今後特性方程式を扱いますが,(5)について,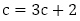 とする方程式は,与えられた漸化式を満たす定数列を探すもので,特性方程式としません。
とする方程式は,与えられた漸化式を満たす定数列を探すもので,特性方程式としません。
【問題3】に与えられる漸化式の一般項は文字係数A,Bを用いて,形だけ確認すると,
順に
(1)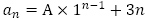 ,
,
(2)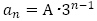 ,
,
(3)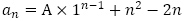 ,
,
(4)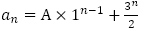 ,
,
(5)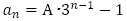 ,
,
(6)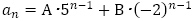 ,
,
(7)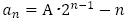
とおくことが可能です。
漸化式から一般項の形を決めることができれば,【問題2】のように,連立方程式を解けばよいことになります。
【問題4】※横浜市立大学 2016年
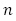 は自然数とする。漸化式
は自然数とする。漸化式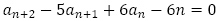 ,
,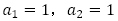 で定められる数列
で定められる数列 の一般項を求めよ。
の一般項を求めよ。
一般項の形は,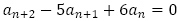 の特性方程式
の特性方程式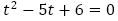 の解
の解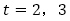 と漸化式
と漸化式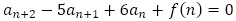 の
の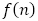 の形に依存しています。一般項は,
の形に依存しています。一般項は,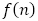 が1次式なので,
が1次式なので,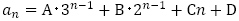 で与えられます。
で与えられます。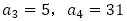 を確認して,連立方程式を解き,
を確認して,連立方程式を解き,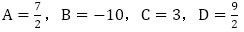 を得ます。したがって,
を得ます。したがって,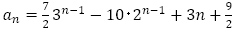 となります。
となります。
一般項の形は,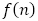 が
が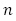 の2次式であれば,一般項も
の2次式であれば,一般項も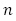 の2次式の形を持ちます。
の2次式の形を持ちます。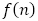 が
が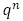 のような指数の形であれば,一般項は
のような指数の形であれば,一般項は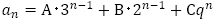 の形となりますが,
の形となりますが,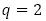 または
または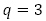 の場合は,
の場合は,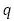 自体を重解とみなして,【問題2】(2)の置き方を採用することとなります。以下,例を扱います。
自体を重解とみなして,【問題2】(2)の置き方を採用することとなります。以下,例を扱います。
【問題5】
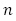 は自然数とする。漸化式
は自然数とする。漸化式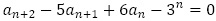 ,
,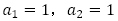 で定められる数列
で定められる数列 の一般項を求めよ。
の一般項を求めよ。
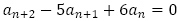 の特性方程式
の特性方程式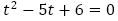 の解
の解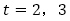 と漸化式に含まれる
と漸化式に含まれる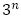 の形から一般項は
の形から一般項は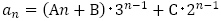 とおいて,
とおいて,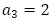 と連立方程式から,
と連立方程式から,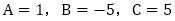 を得ます。したがって,一般項は
を得ます。したがって,一般項は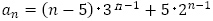 となります。ここまでの多くの内容は有名ですが,これ以降の内容のために必要な予備知識となっています。
となります。ここまでの多くの内容は有名ですが,これ以降の内容のために必要な予備知識となっています。
【問題6】※一般項を求めるわけではないので,初期条件を書きません。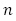 は自然数とします。
は自然数とします。
(1)漸化式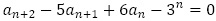 で定められる数列
で定められる数列 が満たす4項間漸化式を求めよ。
が満たす4項間漸化式を求めよ。
(2)漸化式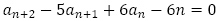 で定められる数列
で定められる数列 が満たす5項間漸化式を求めよ。
が満たす5項間漸化式を求めよ。
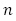 について差分していくことで(1),(2)ともに処理します。
について差分していくことで(1),(2)ともに処理します。
(1)について,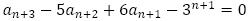 から
から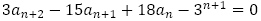 を引いて,
を引いて,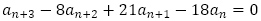 を得ます。
を得ます。
(2)について,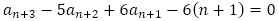 から
から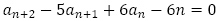 を引いて,
を引いて,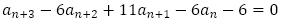 を得ます。さらに,
を得ます。さらに,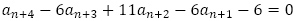 から
から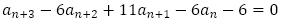 を引いて,
を引いて,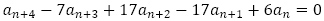 を得ます。
を得ます。
(1)の4項間漸化式の特性方程式は,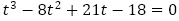 で,
で,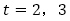 (3は2重解)から一般項は
(3は2重解)から一般項は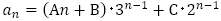 とおけることは確認できます。
とおけることは確認できます。
(2)の5項間漸化式の特性方程式は,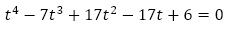 で,
で,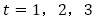 (1は2重解)から一般項は
(1は2重解)から一般項は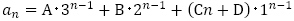 とおけることは確認できます。
とおけることは確認できます。
1次式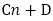 の部分を
の部分を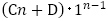 とみるのがポイントです。上記のような操作をするたびに特性方程式の解に
とみるのがポイントです。上記のような操作をするたびに特性方程式の解に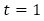 が増えていきます。
が増えていきます。
例えば,一般項に定数項があるような例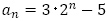 は
は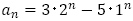 と見れば,
と見れば,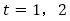 を解に持つ2次方程式
を解に持つ2次方程式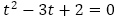 を特性方程式とする漸化式
を特性方程式とする漸化式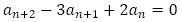 を満たすことが分かります。以上の知識をもとに一般項が与えられた数列が満たす漸化式を復元する方法と,それがどんなときに便利かを確認しておきます。
を満たすことが分かります。以上の知識をもとに一般項が与えられた数列が満たす漸化式を復元する方法と,それがどんなときに便利かを確認しておきます。
【問題7】※千葉大学2013年
整数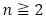 に対して,
に対して,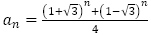 は整数であり,3で割った余りは2であることを示せ。
は整数であり,3で割った余りは2であることを示せ。
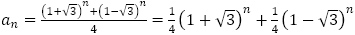 が満たす漸化式は,一般項が
が満たす漸化式は,一般項が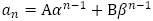 の形であることに注意すると,係数
の形であることに注意すると,係数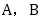 は関係なく,
は関係なく,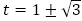 を解に持つ2次方程式
を解に持つ2次方程式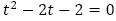 を特性方程式とする3項間漸化式
を特性方程式とする3項間漸化式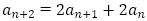 を満たすことが分かります。2019年に早稲田大学商学部の問題で漸化式の復元は実際に出題があります。漸化式から明らかに
を満たすことが分かります。2019年に早稲田大学商学部の問題で漸化式の復元は実際に出題があります。漸化式から明らかに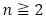 のとき,
のとき,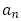 は整数で,漸化式
は整数で,漸化式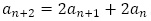 から
から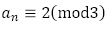 ,
,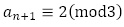 を仮定しての数学的帰納法で【問題7】は処理できます。
を仮定しての数学的帰納法で【問題7】は処理できます。
【問題8】※東京工業大学2013年
2次方程式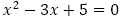 の2つの解
の2つの解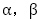 に対し,
に対し,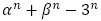 はすべての正の整数
はすべての正の整数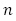 について5の倍数であることを示せ。
について5の倍数であることを示せ。
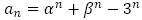 が満たす漸化式は,一般項が
が満たす漸化式は,一般項が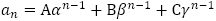 の形であることに注意すると,
の形であることに注意すると,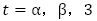 を解に持つ3次方程式
を解に持つ3次方程式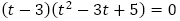 すなわち
すなわち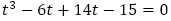 を特性方程式とする4項間漸化式
を特性方程式とする4項間漸化式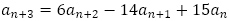 を満たすことが分かります。
を満たすことが分かります。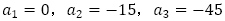 を確認すれば,
を確認すれば,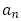 は明らかに5の倍数となることが分かります。整数と漸化式に関する問題は合同式や最大公約数と関連しての出題が多いですが,2021年東京大学でも出題があり,定期的に出題されています。
は明らかに5の倍数となることが分かります。整数と漸化式に関する問題は合同式や最大公約数と関連しての出題が多いですが,2021年東京大学でも出題があり,定期的に出題されています。
【問題9】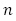 は自然数とする。
は自然数とする。
(1)漸化式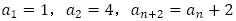 で定められる数列
で定められる数列 の一般項を求めよ。
の一般項を求めよ。
(2)漸化式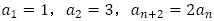 で定められる数列
で定められる数列 の一般項を求めよ。
の一般項を求めよ。
(1),(2)ともに偶奇での場合分けを考えてみます。念のためにそれぞれ書き並べてみると(1) は1,4,3,6,5,8,7,10,・・・・・・,(2)は1,3,2,6,4,12,8,24・・・・・・となります。
自然数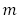 について,(1)では,
について,(1)では,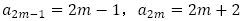 として,(2)では,
として,(2)では,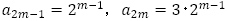 と場合分けしておき,
と場合分けしておき,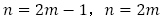 についてそれぞれ
についてそれぞれ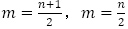 と置き換えて,
と置き換えて,
(1)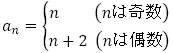 ,(2)
,(2)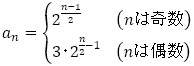 としました。
としました。
数列 の奇数項が
の奇数項が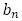 ,偶数項が
,偶数項が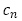 であるとき,
であるとき,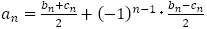 で与えることができるのは有名です。【問題9】のそれぞれの一般項を場合分けせずに書いておくと,
で与えることができるのは有名です。【問題9】のそれぞれの一般項を場合分けせずに書いておくと,
(1)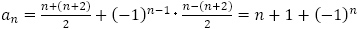
(2)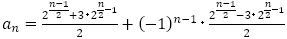 で,整理すると
で,整理すると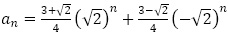
(2)の一般項の形が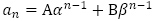 の形であるので,
の形であるので,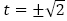 を解にもつ2次方程式
を解にもつ2次方程式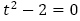 を特性方程式とする漸化式
を特性方程式とする漸化式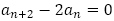 がもとにあるわけで,
がもとにあるわけで,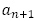 の項がなく隣接していなくても,特性方程式は有用だと分かります。この問題に特性方程式を取らずに偶奇で場合分けをすることは体系的な指導とならないように思います。
の項がなく隣接していなくても,特性方程式は有用だと分かります。この問題に特性方程式を取らずに偶奇で場合分けをすることは体系的な指導とならないように思います。
(1)の一般項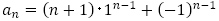 は,
は,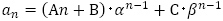 の形であるので,
の形であるので,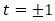 (1が2重解)を解にもつ3次方程式
(1が2重解)を解にもつ3次方程式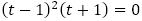 すなわち
すなわち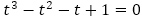 を特性方程式とする漸化式
を特性方程式とする漸化式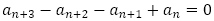 がもとにありますが,【問題9】(1)の漸化式
がもとにありますが,【問題9】(1)の漸化式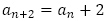 を
を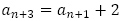 とずらして引けば,4項間漸化式
とずらして引けば,4項間漸化式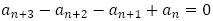 が得られて,ここまでに確認した知識で解くことができます。何項間になっても斉次な漸化式にすれば,一般項の形が決まるわけなので,一般項が求まってしまうような数列は基本的に連立方程式を頑張れるかという一点に帰着されます。以下で,大学入試問題を実際に解いてみようと思います。
が得られて,ここまでに確認した知識で解くことができます。何項間になっても斉次な漸化式にすれば,一般項の形が決まるわけなので,一般項が求まってしまうような数列は基本的に連立方程式を頑張れるかという一点に帰着されます。以下で,大学入試問題を実際に解いてみようと思います。
【問題10】※高知大学2021年
数列 は
は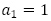 ,すべての自然数
,すべての自然数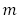 に対して,
に対して,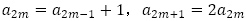 を満たすとする。
を満たすとする。
数列 の一般項を求めよ。
の一般項を求めよ。
偶奇で異なる数列であることは問題からも明らかですが,数列 を書き並べておくと1,2,4,5,10,11,22,23,・・・・・・となっています。数列
を書き並べておくと1,2,4,5,10,11,22,23,・・・・・・となっています。数列 は何かしらの5項間漸化式を満たすはずで,特に偶数列のみ,奇数列のみの3項間漸化式を想定することが可能なので,確認します。
は何かしらの5項間漸化式を満たすはずで,特に偶数列のみ,奇数列のみの3項間漸化式を想定することが可能なので,確認します。
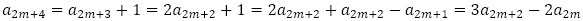
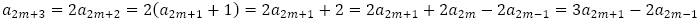
をそれぞれ得ることができて,すなわち,すべての自然数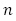 について,数列
について,数列 は隣接しない5項間漸化式
は隣接しない5項間漸化式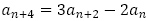 を満たしています。隣接していなくても関係なく,特性方程式は
を満たしています。隣接していなくても関係なく,特性方程式は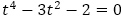 をおいて,解は
をおいて,解は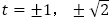 を得ます。したがって,数列
を得ます。したがって,数列 の一般項は
の一般項は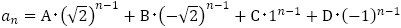 の形だと分かります。
の形だと分かります。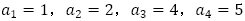 を求め,連立方程式を解き,
を求め,連立方程式を解き,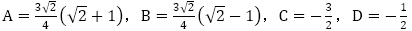 を得て,数列
を得て,数列 の一般項は,
の一般項は,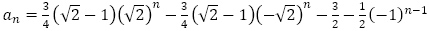 となります。この解答をどのように取り扱うか,同様の出題をするならどのような立場かを明確にしておくべきだと思います。
となります。この解答をどのように取り扱うか,同様の出題をするならどのような立場かを明確にしておくべきだと思います。
【問題11】※群馬大学2007年
数列 は
は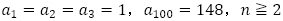 のとき,
のとき,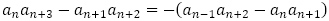 かつ
かつ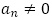 を満たしている。数列
を満たしている。数列 の一般項を求めよ。
の一般項を求めよ。
数列 を書き並べようとすると,
を書き並べようとすると,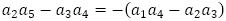 と
と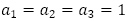 より,
より,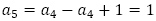 で,以降
で,以降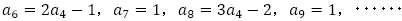 と
と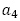 は分からないままですが,数列
は分からないままですが,数列 の
の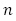 の偶奇で異なる数列から構成されていると分かります。
の偶奇で異なる数列から構成されていると分かります。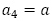 として,
として,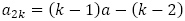 ではないかと帰納法で確認していくことになるはずですが,
ではないかと帰納法で確認していくことになるはずですが,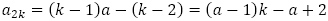 は等差数列で
は等差数列で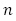 の1次式で書けること,数列
の1次式で書けること,数列 の奇数項が
の奇数項が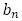 ,偶数項が
,偶数項が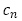 であるとき,
であるとき,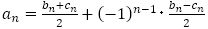 で書けること,
で書けること,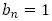 であることに注意すると,
であることに注意すると,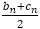 も
も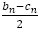 も
も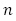 の1次式で書けることになります。
の1次式で書けることになります。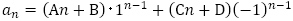 であるはずです。これは数列
であるはずです。これは数列 が
が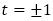 (1,-1ともに2重解)を解とする4次方程式
(1,-1ともに2重解)を解とする4次方程式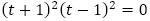 すなわち
すなわち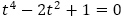 を特性方程式とする漸化式
を特性方程式とする漸化式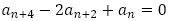 を満たすはずで,目標が決まった変形を問題の漸化式に与えていくことになります。
を満たすはずで,目標が決まった変形を問題の漸化式に与えていくことになります。
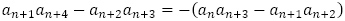 と
と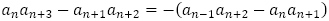 を引き算して,
を引き算して,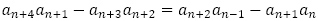 を得ます。両辺に
を得ます。両辺に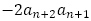 を加えて,
を加えて,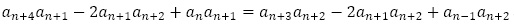 とします。
とします。
よって,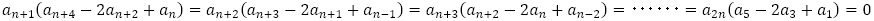 を得て,
を得て,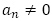 より
より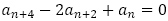 を得ることができました。
を得ることができました。
一般項の形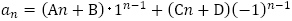 と
と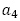 の値がないので,
の値がないので,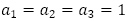 と問題に与えられている条件
と問題に与えられている条件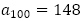 を用いて,連立方程式を解いて,
を用いて,連立方程式を解いて,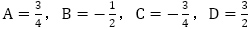 を得て,数列
を得て,数列 の一般項は,
の一般項は,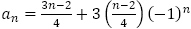 とできます。
とできます。
【問題12】※千葉大学2018年
初項が1で公差が6である等差数列1,7,13,・・・の第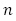 項を
項を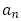 ,初項が3で公差が4である等差数列3,7,11,・・・の第
,初項が3で公差が4である等差数列3,7,11,・・・の第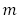 項を
項を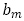 とする。(中略)2つの数列
とする。(中略)2つの数列 ,
,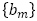 の少なくとも1つの項になっている数すべてを小さい順に並べてできる数列を
の少なくとも1つの項になっている数すべてを小さい順に並べてできる数列を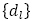 とする。
とする。
(1)略 (2)数列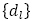 の一般項を求めよ。
の一般項を求めよ。
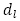 を書き並べてみると1,3,7,11,13,15,19,23,25,27,31,35,37,・・・となっていて,
を書き並べてみると1,3,7,11,13,15,19,23,25,27,31,35,37,・・・となっていて,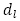 の階差数列を
の階差数列を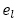 とすれば,
とすれば,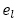 は2,4,4,2を繰り返していることが分かります。したがって,
は2,4,4,2を繰り返していることが分かります。したがって,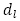 も周期4の規則性を保っていることに着目すると,
も周期4の規則性を保っていることに着目すると,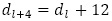 を得ます。
を得ます。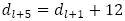 と引き算をして,
と引き算をして,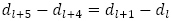 として,特性方程式
として,特性方程式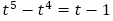 から,
から,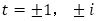 (1は2重解,
(1は2重解,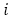 は虚数単位)を得ます。
は虚数単位)を得ます。
したがって,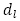 の一般項は
の一般項は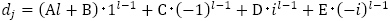 の形だと分かります。
の形だと分かります。
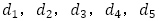 の値を用いて連立方程式を解くと,
の値を用いて連立方程式を解くと,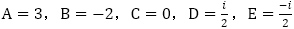 を得て,数列
を得て,数列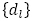 の一般項は,
の一般項は,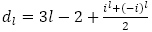 とできます。
とできます。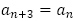 のような漸化式は2020年の琉球大学で出題がありました。これも場合分けすることなく,
のような漸化式は2020年の琉球大学で出題がありました。これも場合分けすることなく,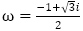 を用いることで,一般項を 1本の式で書くことが可能です。
を用いることで,一般項を 1本の式で書くことが可能です。
授業において3項間漸化式を解くことだけを考えると,一般項の形を決めてしまい,係数を連立方程式によって求める方法は生徒にとって非常に理解の良いものでした。3項間漸化式を満たす数列の一般項の多くがなぜ等比数列の一般項の和や差として決まるのかを説明する上で,教科書にあるような変形は非常に重要です。変形による解法を蔑ろにして良いものではないと考えます。係数決定による方法を紹介することで,生徒は飛躍的に早く解答にたどり着くことが可能になります。係数決定によって一般項は定めるという感覚は共通テストなどの穴埋め形式のテストにも非常に有効です。
漸化式の一般項を求めること自体は,そもそも解ける漸化式なのですから,どんなに式を複雑にしても難しいものではありません。一般項から漸化式を復元できて,教員として一番便利なのは生徒に答えさせたい答えから,問題を作れることです。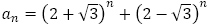 や
や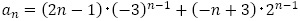 が満たす3項間漸化式や5項間漸化式が求められるというのは,数学的な楽しみが増えるように思います。一般項を偶奇で場合分けして答えさせたいような問題を出題するなら,4項間以上の漸化式の処理について事前に指導があっても良いのではないかと考えます。
が満たす3項間漸化式や5項間漸化式が求められるというのは,数学的な楽しみが増えるように思います。一般項を偶奇で場合分けして答えさせたいような問題を出題するなら,4項間以上の漸化式の処理について事前に指導があっても良いのではないかと考えます。