HP上，本校で実践を進めてきた学校設定科目データサイエンスⅠ（DSⅠ），データサイエンスⅡ（DSⅡ）からの実践報告を行ってきた，第3回目である。第1回は，「散布図・相関係数」を取り上げた。第2回目は，「仮説検定」について実践報告を行った。第3回は，条件付き確率の応用としてベイズ統計学の入門の実践を行ったので報告する。
なお本報告は，勤務校である神戸大学附属中等教育学校の中等論集，4，27-32「魅力ある統計教育の教材開発2」の内容を再構成したものである。
令和3年の学習指導要領改訂以前より，場合の数・確率において「条件付き確率」の学習項目は存在していたものの，今までは現場ではあまり重要視されてこなかったように感じている。
しかし，covid-19の世界的流行とともに，検査の結果に対する「偽陽性」「偽陰性」という言葉が一般に知られるようなった。「偽陽性」「偽陰性」は，条件付き確率の話題であり，確率・統計が社会で使われている例として授業で扱うことが出来た。
まず，本取り組みで最重要の定理である「ベイズの定理」を，どのように授業で導出したか説明する。
全事象Uの中の2つの事象AとBについて，
事象Aが起こることが起こる条件のもと，Bが起こる確率を，Aが起こったときのBの条件付き確率といい，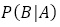
で表す。
ただし，高等学校数学Aの教科書では，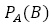
で表現するが，本報告では，より一般的な表記である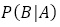で表現する。
条件付き確率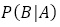は，全事象をAとしたときのBが起こる確率であるので，
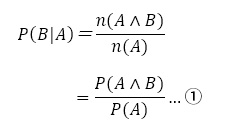
となる。
ここで，①より
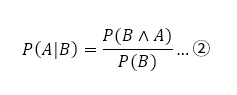
が得られる。また，
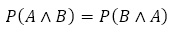
と，①，②より次の定理が得られる。
ベイズの定理
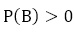のとき
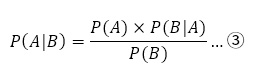
また，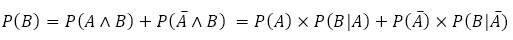
であるので，③の別表記が得られる。
ベイズの定理
のとき
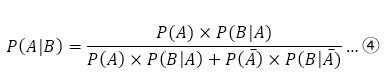
一般的に，Aに観測事象，Bにそれが起因である原因の事象になるので，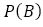
を直接求めることができない。
しかし，Bの起こりうることを場合分けし求めることにより，④が導出できる。
【実践内容】
教科書での基本的な条件付き確率の指導が終わった後，ベイズの定理の証明とその利用に入った。なお，取り扱う問題は，「見えないものをさぐる―それがベイズ: ツールによる実践ベイズ統計(オーム社)」を参考にした。
まず，問題1に取り組んだ。
問題1 (1)
ある病気を発見する検査法は，その病気の患者が受けると99%の人が陽性反応を示します。
しかし，その病気でない健康な人でも3%の人が陽性反応を示し，誤った診断を下してしまいます。
日本国内で，その病気の患者の割合は0.1%であることが分かっています。
さて，日本に住むEさんがこの検査を受けたら陽性反応がでました．Eさんがその病気である確率は何%ですか。
まず，ベイズの定理を用いずに確率を求める方法に授業を展開した。
[解答]ベイズの定理を用いない方法
まず，日本国内の人口を100,000人とする。
すると，以下のように場合分けができる。
① 病気の人が検査を受ける場合
陽性：100×0.99=99(人)
陰性：100×0.01=1(人)
② 病気でない人が検査を受ける場合
陽性：99,900×0.03=2,997(人)
陰性：99,900×0.97=96,903(人)
求める確率は，
であり，陽性の中で病気の人は，病気の人の中で陽性の人であるので，
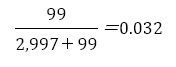
よって，3.2%。(終)
グループ活動で上記を求めさせたが「病気の人の中で陽性」「病気の人の中で陰性」「病気でない人の中で陽性」「病気でない人の中で陰性」の人数を求めたのちに求める確率を計算するように指示をしたところ，ほとんどのグループが求値できていた。この問題1(1)の指導後にベイズの定理④の導出を行った。
なお，最初に日本に100,000人いるとして確率を求値したが，即ベイズの定理を用いるよりも下記の点でよいと考えられる。
1回目の検査で陽性の人が病気である確率が3.2%と，あらかじめ予想した値よりも低い理由が
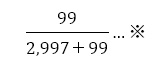
の2,997が大きく影響していることが一目瞭然であり，また病気でない人のうち陰性判定する確率が3%であることに起因していると多くの生徒が実感できたと考えられる。
上記の※の式より
であることが強く意識づける指導が可能となり，
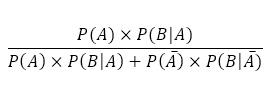
が，数式の意味を理解させるように心がけた。
また，
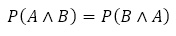
の関係を意識させるために を全体指導において強調した。次に問題1をベイズの定理を用いて解く前に，問題2を練習として挟んだ。
問題2
ある学年に生徒が100人います。学年の生徒の中でカメラと時計の両方を持っている確率を求めたい。
この学年の中の御影さん，住吉さん，明石さんの3人に，100人の中でカメラと時計を所有している人をそれぞれ調べてもらいました。
この3人の中の情報で，学年の生徒の中でカメラと時計の両方を所持している確率を求められるものはどれか。
[解答]
全事象：学年全員
事象A：時計を持っている人
事象B：カメラを持っている人
御影さん
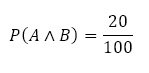
住吉さん
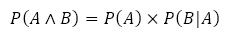
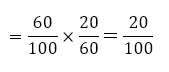
明石さん
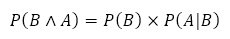
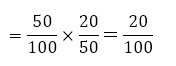
よって，3人全員の調査から求める確率を求めることができる。(終)
問題2の難易度は平易であるが，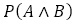
を2種類の条件付き確率
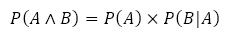
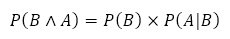
を用いて表すことを具体例で実感させることを目的としている。その後，ベイズの定理を上記に記述した方法で，全体共有を行った。
ベイズの定理を導出したので，問題1(1)をベイズの定理を用いる方法の全体共有を行った。
[解答]ベイズの定理を用いる方法
事象A：Eさんが病気である
事象B：陽性である
求める確率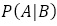
は
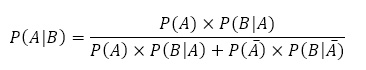
であるので，これに代入する。
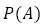：(検査を受ける前の)Eさんが病気である確率
→Eさんは日本に住んでいるので，0.001
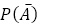：上記より0.999
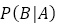：(Eさんが)病気であるときに，陽性である確率→0.99
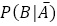：(Eさんが)病気でないときに，陽性である確率→0.03
よって，
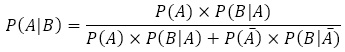
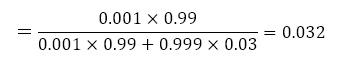
よって，3.2%。(終)
上記にあるように，問題1(1)のベイズの定理を用いる解法と，用いない解法の間に問題2を挟み，ベイズの定理の理解を深めるように心掛けた。
問題1(2)
(1)の検査で陽性反応を示したので，心配になったEさんは，最初の検査を受けた病院で紹介状を書いてもらい，別の病院で検査を受けることにしました。
この病院の検査は以下の通り。
Eさんがこの病院で検査を受けると再度陽性反応を示した。このとき，Eさんが病気である確率は何%か？
問題1(2)は，ベイズの定理による確率更新(ベイズ更新)を理解させる狙いがある。問題1(1)で求めた事後確率3.2%を(2)では事前確率にするところがポイントである。求めた事後確率を次の事前確率に用いることを理解させたい。
[解答]
事象A：Eさんが病気である
事象B：陽性である
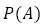：(2回目の検査を受ける前の)Eさんが病気である確率
→Eさんは1回目の検査で陽性反応を示し，病気である確率が，0.032と求まったので，これを事前確率に用いる。
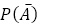：上記より0.968
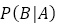：(Eさんが)病気であるときに，陽性である確率→0.98
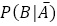：(Eさんが)病気でないときに，陽性である確率→0.02
よって，
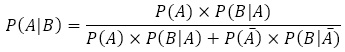
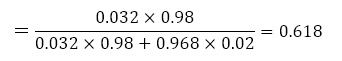
よって，61.8%。(終)
2回目の検査は，紹介状を持って来院しなければ検査が受けられない状況で，また2回連続で陽性反応を示したことにより，Eさんが病気である確率が急に上がった様子を共有した。
また，この時点でベイズの定理と確率更新について以下の注意を全体に行った。
注意1
ベイズの定理は，
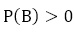のとき
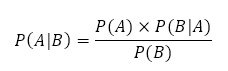
であるが，
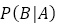は，Aが起こる前提でBが起こる確率
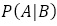は，Bが起こる前提でAが起こる確率
であり，片方が求まっていると，その逆向きが求まることを示している。
注意2
注意3
観測のたびに，0.1%から3.2%へ，3.2%から61.8%へと確率が更新されていっている。このように，観測を行いながら事後確率を更新していくことをベイズ更新という。
最後に発展的な話題として以下の問題を取り扱った。
問題3
村はずれの羊使いの少年が，退屈だったのでオオカミがいないのに，「オオカミがきたぞ！」とウソをついて騒ぎを起こします。
村人たちは，これは大変とオオカミ退治に向かいますが，いくら探しても肝心のオオカミがいません。これをおもしろがった少年は，このウソを繰り返します。
ところがある日，本当にオオカミがやってきました。
少年は「オオカミがきたぞ！」と伝えましたが，村人はもうその少年の言葉を信用せずオオカミ退治に行かなかったため，村の羊はすべてオオカミに食べられてしまいました。 （イソップ童話「オオカミ少年」より）
(1) 村の代表者である村長は，何回目のウソでこの少年を信用しなくなったのか？
ここまでベイズの定理を扱ってきたが，少年が「オオカミがきたぞ！」といったが，オオカミがこなかった理由に「少年がウソをついたことにより村人はオオカミと出会えなかった」場合以外に，「少年は本当のことを言ったが，(なんらかの理由で)村人はオオカミと出会えなかった」ことがある。特に後者の可能性があることは，丁寧に全体共有する必要がある。
また，後述する各種条件の正確な確率は求めることができないので，主観確率とよばれる主観的な確率を設定し，ベイズの定理で確率を更新していく。また，少年は「オオカミがきたぞ！」とウソをつき続けるものである(途中で本当のことを言わない)ことも全体で十分に確認しておく必要がある。
なお，生徒に
と問いかけてみると，前者は0.1，後者は0.9という返答が多かったため，今回は事前確率を0.1，0.9を超えると村長はAをウソつきと判定することにする。
[解答]
事象A：少年はウソつき
事象B：オオカミはやってこない
あらかじめ必要な事前確率と条件付き確率を設定する。
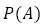：少年がウソをつく以前，村長が「少年はウソつきだ」と思う事前確率(主観)→0.1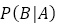：少年がウソつきであったとき，オオカミがこない(村人はオオカミと出会えない)確率→0.95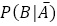：少年が本当のことを言ったとき，オオカミがこない(村人はオオカミと出会えない)確率→0.3この設定で，オオカミと出会えないとき，少年がうそつきである(うそつきであることに起因する)確率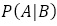は，
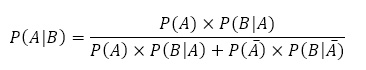
から求める。
また，2回目以降の事前確率は，その1回前の事後確率を用いる。
すると，
この手順で帰納的に事後確率を求める。
1回目:26.0%
2回目:52.7%
3回目:77.9%
4回目:91.7%
5回目:97.2%
6回目:99.1%
7回目:99.7%
よって，0.9(=90%)を超えるとウソつきと判定することにするならば，4回ウソをついたときである。(終)
(2) もし，初回が「本当」の場合(すなわち，少年は本当にオオカミを発見し，実際に村人がオオカミと出会えた場合)，その後少年はウソをつき続けてオオカミと出会えなかった場合，何回目のウソで村長はこの少年を信用しなくなったのか？
この問題のポイントは，以下の2点である。
事象A：少年はウソつき
事象B：オオカミはやってこない
を用いてどのように記述するのか，である。
[解答]
最初に本当のことをいい，実際にオオカミと出会えたので，
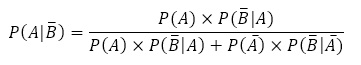
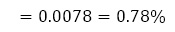
これを用いて，(1)と同様に計算すると，
1回目:2.5%
2回目:7.4%
3回目:20.1%
4回目:44.9%
5回目:71.6%
6回目:88.9%
7回目:96.2% となる。
よって，0.9(=90%)を超えるとウソつきと判定することにするならば，7回ウソをついたときである。(終)
(3) 一度も少年は本当のことを言わなかったとき，村長は，少年の何回目のウソでオオカミ退治に「行かない」選択をすべきか．損失の期待値を計算することで判断しなさい。
本来は，条件付き確率で処理をする方がより正確ではあるが，簡便的に損失の期待値を以下のように計算した。
① オオカミ退治に「行かない」選択をした場合
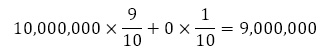
② オオカミ退治に「行く」選択をした場合
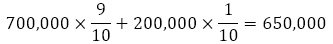
したがって，この場合は，オオカミ退治に「行く」選択をすべきである。
同様に
| 損害の期待値 | ||
|---|---|---|
| 行かない場合 | 行く場合 | |
| 1回目のウソの後 | 7,398,000円 | 569,900円 |
| 2回目のウソの後 | 4,730,000円 | 436,500円 |
| 3回目のウソの後 | 2,209,000円 | 310,450円 |
| 4回目のウソの後 | 822,000円 | 241,100円 |
| 5回目のウソの後 | 275,000円 | 213,750円 |
| 6回目のウソの後 | 89,000円 | 204,450円 |
| 7回目のウソの後 | 29,000円 | 201,450円 |
6回目のウソの後では，損害の期待値がオオカミ退治に「行かない」場合よりも「行く」場合の方が高いことが分かる。
したがって，7回目以降の「オオカミがきたぞ！」という連絡には応じなくてもよい。(終)
授業の展開としては，
などが想定される。
また，エクセルやプログラムを用いて様々なシュミレーションを行った生徒もいた。
統計・データサイエンスの視点からは，数学Ⅰ「データの分析」，数学B「確率分布と統計的な推測」にどうしても注目されがちであるが，ベイズ統計の基礎である条件付き確率の授業実践を今回は紹介した。実践の機会を与えてくださった勤務校である神戸大学附属中等教育学校，熱心に授業を受けてくれた同校9回生の生徒，またこのような紹介の場を提供してくださった新興出版社啓林館の皆様に感謝の意を表する。
【参考文献】
