

本校は令和元年度からSSH(スーパーサイエンスハイスクール)の指定校になっている。数学でもSSC数学班という部活動があり,週に1回程度の活動を行っている。
内容は以下の通りである。
数学班では数学に興味を持っている生徒が多いため,生徒は意欲的に取り組んでいる。ここでは夏休みに実施したSSH数学公開講座の内容を紹介し,実際に講座を受けた生徒の感想も載せる。また最後にこの講座の意義についても述べる。
| 講 座 名: | SSH数学公開講座「黄金比」 |
| 日 時: | 令和2年8月21日(金)及び25日(火) |
| 時 間: | 毎回約2時間(計4時間)(興味がある一部の生徒にはさらに2時間) |
| 対 象: | 1,2年生 16名+理科教員2名 |
| 配布資料: | A4で約60ページ |
| 内 容: | 黄金比 |
前 編
(1)ユークリッドの問題から
(2)ペンタグラマの中に現れる黄金比
(3)黄金比と正五角形の作図
(4)もうひとつの比-白銀比-
(5)黄金長方形-正方形がいくつとれるか-
(6)フィボナッチ数列と黄金比
(7)フィボナッチ数列とパスカルの三角形
(8)対数螺旋と黄金比
(9)連分数
(10)黄金比の連分数展開
(11)連分数による有理数近似
(12)黄金比は最も有理数を寄せ付けない
(13)植物の葉の並びと黄金比
(14)ひまわりと松ぼっくりにでてくる螺旋
後 編
(15)黄金比にさらなる数学的メスを入れる
(16)フィボナッチからの分数列が最も黄金比に近いことの証明
(17)T 値で黄金比に近づく数列を分類する
(18)フィボナッチからの分数列が黄金比に近づく速さ
(19)黄金比の周りの有理数分布
(20)白銀比に数学的メスを入れる
(21)白銀比とペル数
(22)ペル数による分数列が白銀比に近づく速さ
(23)青銅比に数学的メスを入れる
(24)分数列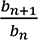 が青銅比に近づく速さ
が青銅比に近づく速さ
(25)貴金属比の中の黄金比
(26)神様が造った黄金比が自然を操る
この段階で,1,2年生とも数列や極限をまだ習っておらず,ある程度感覚的にわかるように資料を作成した。「収束」等の用語もここでは使用せず,厳密性について不十分なところはいくつかあるが,高校1年の生徒でもわかる内容となっている。前編では(1)から(14)を掲載する。(15)以降は後編に載せるが,後編は数学を本格的に駆使し,厳密性を増してかかれている。以下は生徒に配布したプリントである。
なお,ここでは,「比の値」を単に「比」とよぶことにする。
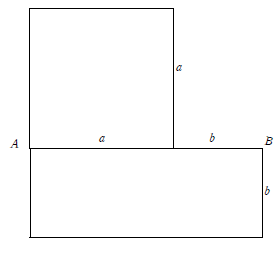
歴史上初めて黄金比について言及したのはユークリッドである。次のような問題をだした。
【問題】
線分AB をa:b に分け,次のように正方形と長方形をつくる。2つの面積が等しくなるとき,a:b を求めよ。
【解説】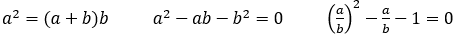
【答え】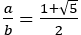
15世紀後半,イタリアの数学者ルカ・パチョーリはこの比を「神の比」と名付けた。
「この比は数理的に割り切ることのできない比で,言葉で限定しがたく,それ自身として存在し,神のごとくユニークであり,神意によって天から授けられたものである」と述べている。
昔からヨーロッパでは正五角形の頂点を1つおきに結んでできる星形を「ペンタグラマ」とよんで徳の象徴として考えてきた。このペンタグラマの中にも黄金比が出てくる。実際それの黄金比は正五角形の対角線で作られる二等辺三角形の辺の比に現れる。
具体的には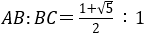 である。
である。
なぜなら・・・
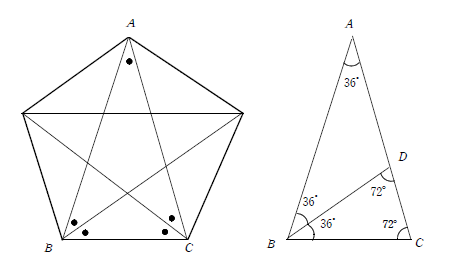
正五角形は円に内接し,円周角の定理から●はすべて等しくなる。三角形の内角の和が180°であるから●=36°である。
AB=x BC=1とする。BC=BD=AD であるからCD=x−1
ΔABC∽ΔBCDよりx:1=1:(x−1)
これより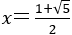
【問題】
AB=1のとき,黄金比の長さをもつ線分を作図しなさい。
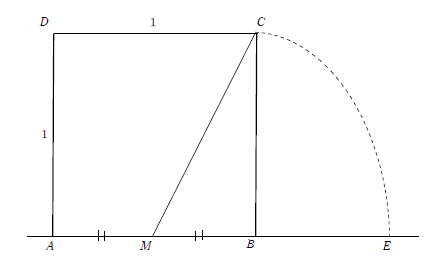
【解説】
ABを一辺とする正方形を考える。
ABの中点をMとする。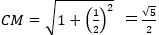
Mを中心に半径CMの円をかき,ABの延長との交点Eをとれば
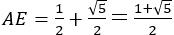 となる。
となる。
【問題】
AB=1とする。一辺がABである正五角形を作図しなさい。
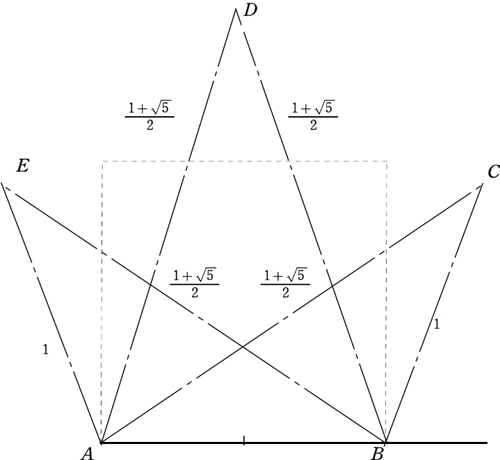
【解説】
長さが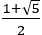 と1の線分を上記のように組み合わせて三角形をつくり,その頂点をC,D,Eとすれば,五角形ABCDEが求めるもの。
と1の線分を上記のように組み合わせて三角形をつくり,その頂点をC,D,Eとすれば,五角形ABCDEが求めるもの。
【問題】
半径1の円に内接する正五角形を作図しなさい。
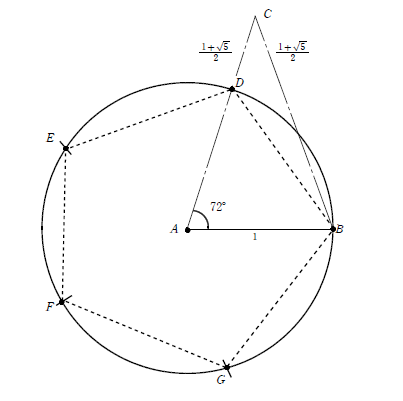
【解説】
まずAを中心として半径1の円をかく。図で∠BAD=72°であることを利用。
AB(=1)を底辺として側辺が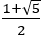 であるような二等辺三角形ABCを作図する。
であるような二等辺三角形ABCを作図する。
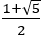 は前の作図を利用する。このときACと円との交点をDとすると,
は前の作図を利用する。このときACと円との交点をDとすると,
∠BAD=72°になることは明らかである。
BDの幅をコンパスで測り,その幅で円周上にDからE,EからF,FからGと点を打っていく。
BDEFGを結んだものが正五角形になる。
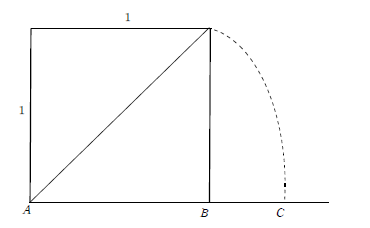
正方形の対角線を半径にAを中心に円をかきABの延長との交点をCとする。
このとき を白銀比という。
を白銀比という。
黄金比の場合はABの中点Mが円の中心であったが,Aが円の中心である。
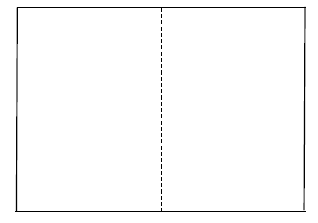
【問題】
縦横の比が白銀比の長方形を半分に折ると・・・縦横の比は?
【解説】
縦横の比は変わらず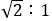 。つまりこの長方形は半分に折っても元の長方形に相似である。世の中で最も多く使われる A 版の紙はこの比である。A 判は,19 世紀末ドイツの物理学者ヴィルヘルム・オストヴァルトによって提案されたドイツの規格で,面積が1 平方メートルの白銀比の長方形をA0 とした。現在では国際規格サイズであり,面積が1m2の白銀比の長方形は縦横が841mm×1189mm である。ノートや教科書など,ほとんどの紙はこの比でできている。
。つまりこの長方形は半分に折っても元の長方形に相似である。世の中で最も多く使われる A 版の紙はこの比である。A 判は,19 世紀末ドイツの物理学者ヴィルヘルム・オストヴァルトによって提案されたドイツの規格で,面積が1 平方メートルの白銀比の長方形をA0 とした。現在では国際規格サイズであり,面積が1m2の白銀比の長方形は縦横が841mm×1189mm である。ノートや教科書など,ほとんどの紙はこの比でできている。
日本では,面積が 1.5 平方メートルの白銀比の長方形をB0とした。例えばA4とB4 で,相似比は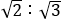 であり,A4 の対角線の長さと,B4の横(長い方の辺)は長さが等しい。B 版は国際的には一般的な規格として知られていない。
であり,A4 の対角線の長さと,B4の横(長い方の辺)は長さが等しい。B 版は国際的には一般的な規格として知られていない。
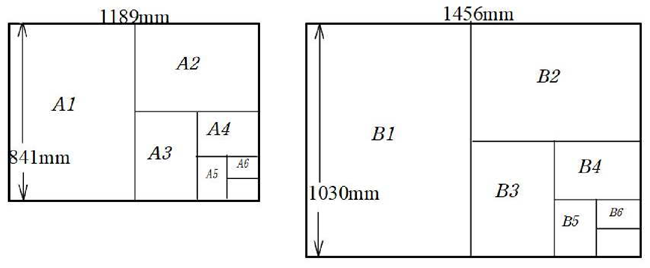
この白銀比は古来から日本で好まれて使われていた。その意味で,白銀比を「大和比」とよぶこともある。例えば法隆寺金堂や五重の塔,銀閣寺の屋根で,上と下で長さの比はそれぞれ白銀比に等しい。また近代的建物にも使われている。例えば東京スカイツリーでは地上から特別展望台の高さと全長の比が白銀比である。

黄金比の長方形では分割についてどんなことがいえるか。
ABFEが正方形になるようにとる。このとき長方形ABCDと長方形EDCFは相似になる。
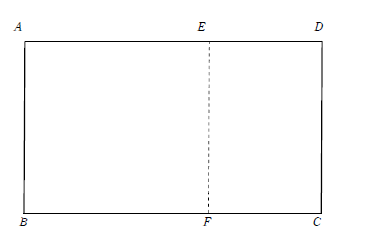
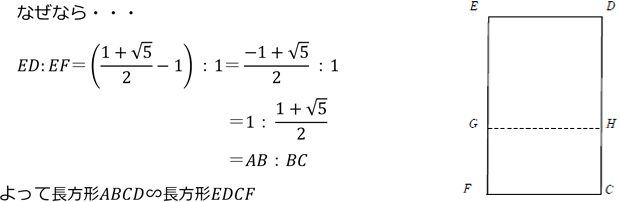
すると長方形EFCDについても同じことがいえる。
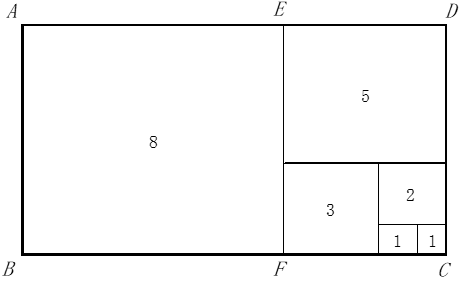
つまり再びこの長方形から正方形をとったら長方形 GFCHは黄金比の長方形である。すると連鎖的に,次のように正方形を並べることができる。

図で は正方形
は正方形 は縦横が黄金比の長方形であるが,ここでは近似的に
は縦横が黄金比の長方形であるが,ここでは近似的に も
も と同じ大きさの正方形と考える。どちらの小さい正方形も一辺の長さを1と考えよう。長方形がかなり小さくなっているから“許してしまおう。”
と同じ大きさの正方形と考える。どちらの小さい正方形も一辺の長さを1と考えよう。長方形がかなり小さくなっているから“許してしまおう。”
このとき図の中の数値は正方形の一辺の長さになる。次は 13 である。

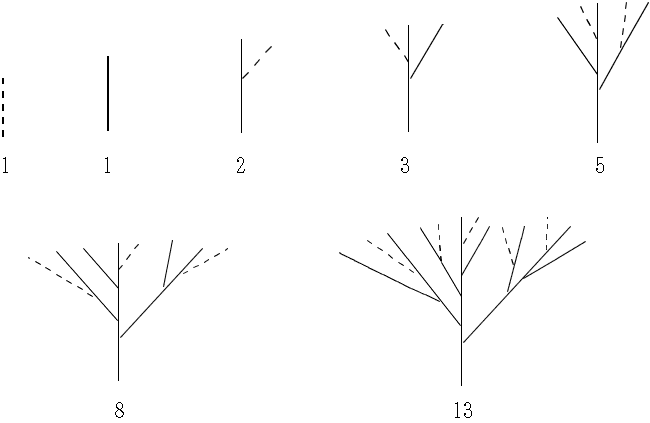
数列 1,1,2,3,5,8,13・・・はフィボナッチ(Fibonacci)の数列とよばれる。イタリアの数学者フィボナッチ(本名:レオナルド・ダ・ピサ)は13世紀初頭,次のように意味づけしてこの数列を世に送り出した。
 は一対の子どものウサギ,
は一対の子どものウサギ, は一対の大人のウサギ
は一対の大人のウサギ
一対の子どものウサギは,一定期間後に一対の大人のウサギになる。その後死ぬことなく,一定期間ごとに一対の子どものウサギを生む。新たに生まれた一対の子どものウサギも同様なステップを踏む。
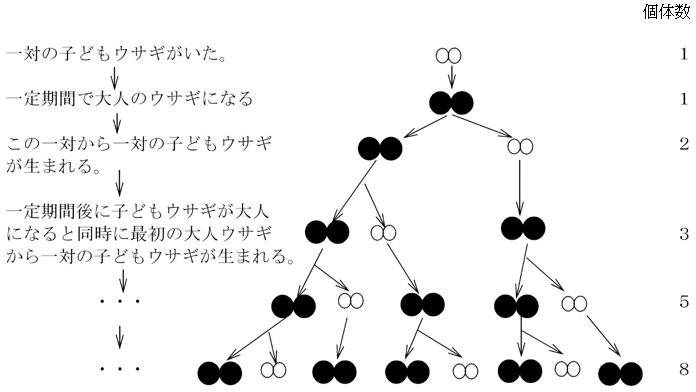
上図の8対のウサギは,5対の大人のウサギと,3対の子どものウサギからなる。5対の大人は明らかに1つ世代前のウサギの対の数に一致。3対の子どものウサギが生まれたのは,2つ世代前のウサギが 3対だったからである。
つまり8=5+3である。
n番目の数を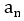 その次はn+1番目で
その次はn+1番目で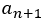
そしてその次は n+2番目で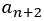 と表記しよう。すると,
と表記しよう。すると,
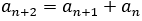 という関係式が成り立つ。これは,
という関係式が成り立つ。これは,
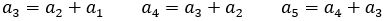 ・・・というように続くことを意味している。フィボナッチの数列は,
・・・というように続くことを意味している。フィボナッチの数列は,

で定義される数列である。
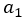 から具体的にかくと,1,1,2,3,5,8,13,21,34,55,89・・・となる。
から具体的にかくと,1,1,2,3,5,8,13,21,34,55,89・・・となる。
ウサギの場合はそのうち先祖となるウサギは亡くなるため,ウサギの頭数はフィボナッチの数列に従うとはいえない。しかし,自然界において,植物の枝の本数は,フィボナッチの数列に従うことがある。
すなわち,若枝が1本生まれ,それが大人の枝へと成長し,その枝から新しい若枝を生えさせる。若枝も,大人の若枝になるが,以前からの大人の枝も含め,大人の枝は一定期間ごとに新しい若枝を生えさせる。
植物の枝の本数ばかりでなく,種子や花びらの枚数もフィボナッチ数列の数になっていることが多い。
(次の写真を参照) 若枝
若枝  大人の枝
大人の枝

花びら2・4~5枚:https://www.s-hoshino.com/kiyaku.html(フリー素材屋Hoshino)
花びら3枚:https://www.photock.jp/detail/flower/2065/(フリー写真素材 フォトック)
ここで,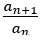 を考える。
を考える。
具体的には,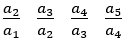 ・・・を考える。
・・・を考える。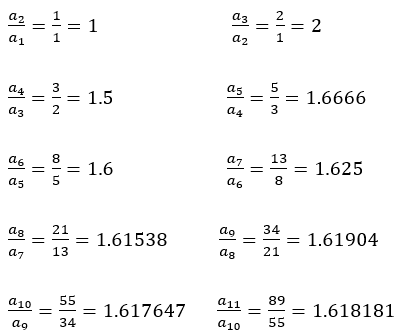
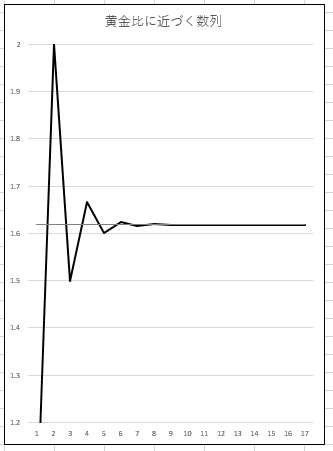
ところで黄金比は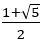 =1.6180339であり,この黄金比に近づいているのがわかる。つまり,
=1.6180339であり,この黄金比に近づいているのがわかる。つまり,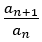 は黄金比に近づく。
は黄金比に近づく。
なぜだろうか。
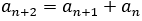 から
から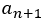 で割って
で割って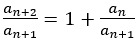
さらに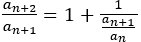 と変形され
と変形され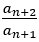 と
と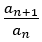 は同じ値に近づくから,その値をxとすれば,
は同じ値に近づくから,その値をxとすれば,
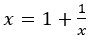 となり
となり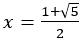 を得る。
を得る。
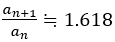 から,最初のいくつかの項を除けば,フィボナッチの数列は次の項を得るのに,ほぼ,1.618倍すればよいことがわかる。
から,最初のいくつかの項を除けば,フィボナッチの数列は次の項を得るのに,ほぼ,1.618倍すればよいことがわかる。

もう少しこの数列について掘り下げて考えてみよう。
実はこの数列は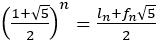 における
における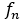 に一致する。
に一致する。
実際,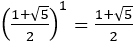 より
より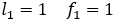
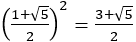 より
より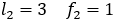
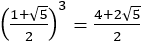 より
より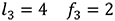
となっている。この後も数列が一致することが次のように確かめられる。
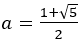 とおくとき,
とおくとき,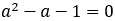 が成り立つので
が成り立つので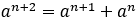
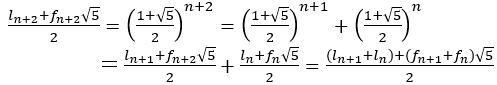
よって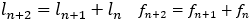 が成り立つ。ここでは,
が成り立つ。ここでは,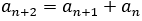 を満たす数列を「フィボナッチ型」とよぶことにする。
を満たす数列を「フィボナッチ型」とよぶことにする。
特に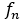 はフィボナッチ型で
はフィボナッチ型で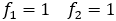 なので,フィボナッチの数列である。
なので,フィボナッチの数列である。
ちなみに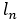 については,
については,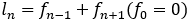 が成り立つ。
が成り立つ。
なぜなら,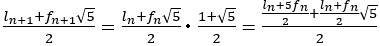
これより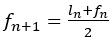
よって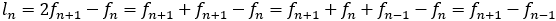 が成り立つ。
が成り立つ。
確かに,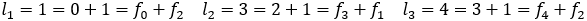 が成り立っている。
が成り立っている。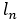 はリュカ数とよばれている。(1, 3, 4, 7, 11・・・)
はリュカ数とよばれている。(1, 3, 4, 7, 11・・・)
それではn番目のフィボナッチ数列やリュカ数を求めよう。
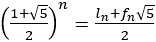 から
から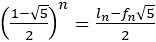 もいえるので,
もいえるので,
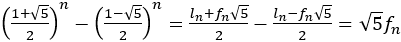 と計算できる。よって次のように表せる。
と計算できる。よって次のように表せる。
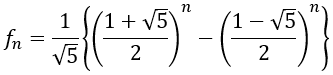
また,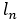 については,
については,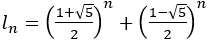 が成り立つ。
が成り立つ。
さて,黄金比に近づく分数は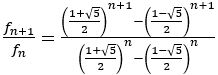 と表せる。
と表せる。
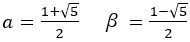 とおくと
とおくと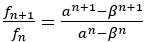
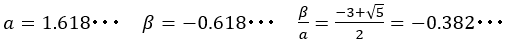 であるので,
であるので,
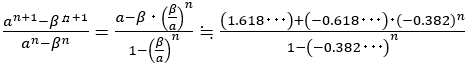
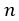 を限りなく大きくすると
を限りなく大きくすると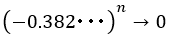 なので,
なので,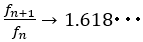 つまり
つまり
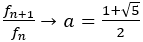 となる。
となる。
この事実は既に述べたものであるが,証明がより数学的になっている。さらに,
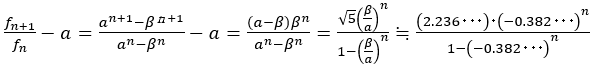 から分母は正,分子は正負を繰り返すことから
から分母は正,分子は正負を繰り返すことから
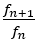 は
は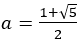 より大きくなったり小さくなったりを交互に繰り返し
より大きくなったり小さくなったりを交互に繰り返し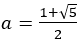 に近づくことがわかる。
に近づくことがわかる。
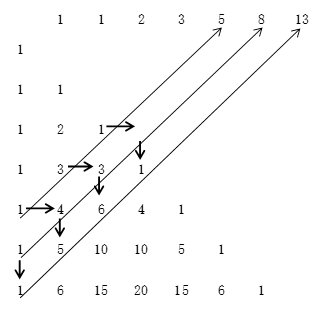
ところでこのフィボナッチの数列は,パスカルの三角形にも現れる。
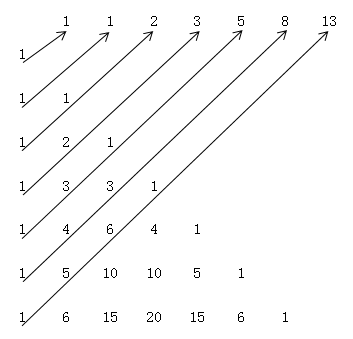
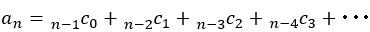 ただし,
ただし,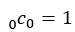
この数列が本当にフィボナッチの数列になるのか具体的にいくつか書き上げて確かめよう。最初の6項は以下の通りである。そして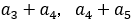 を計算してみる。
を計算してみる。
変形には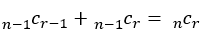 を使う。
を使う。
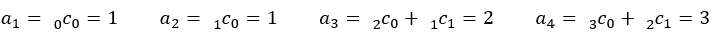

隣接項をたすと・・・
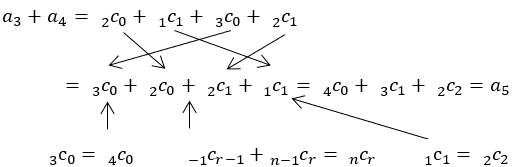
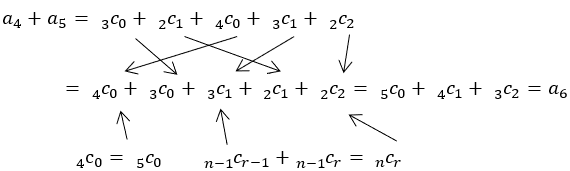
確かに が成り立っている。
が成り立っている。
一般の の場合も式で証明できるが,下のような図を用いれば視覚的に理解できる。
の場合も式で証明できるが,下のような図を用いれば視覚的に理解できる。
パスカルの三角形の上2つの項をたすとその下の項になることを考えれば,図から明らかに示せる。図は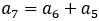 を示したものである。
を示したものである。
さてもう一度黄金比の長方形に戻ろう。正方形の配置を少し変えて,小さな黄金比の長方形が中に入るようにしている。そして各正方形の一辺を半径とする中心角が 90°の円弧をかいていく。すると巻き貝のような螺旋が現れる。
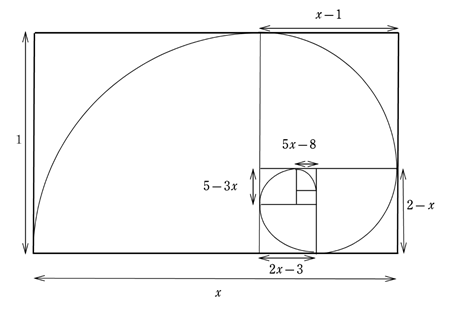
円弧の半径は正方形の一辺なので,黄金比の値をx(長方形の横の長さ)として各正方形の一辺をxで表していく。正方形の一辺の長さは次のように前の2つの式の差から次の式が生まれる。まず1とx-1から次のように計算される。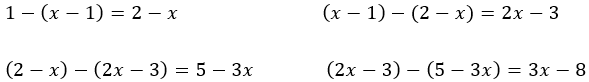
一辺の長さは大きい順に,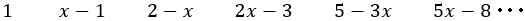
式の係数にフィボナッチの数列が出てくるのが面白い。
フィボナッチの数列1,1,2,3,5,8,13・・・をそれぞれ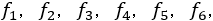 ・・・とし,さらに
・・・とし,さらに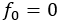 とすれば,次のように表現できる。
とすれば,次のように表現できる。
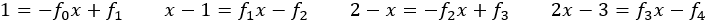
 と表される。
と表される。
そしてこれらを半径とする円弧で,組み立てられている。ところが,
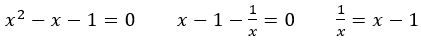 より,
より,
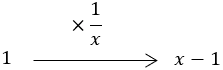
また,x−1から2−xも図形として相似になっているので,
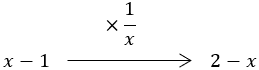
同様に,
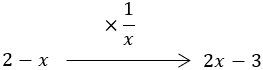
と,この後も続いていく。
あるいは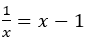 より,
より,
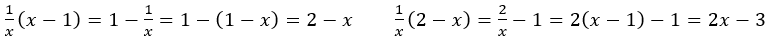
などと変形してもよい。
いずれにしても最初の正方形の一辺が1なので,次のような正方形の一辺の長さになる。
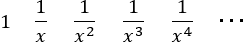
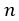 番目の正方形の一辺は
番目の正方形の一辺は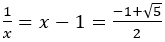 であるので,
であるので,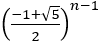 である。
である。
そしてこれが,90°ごとに変わる円弧の半径である。
逆に一辺が1の正方形から出発して次の図のように長方形を組み立てて螺旋をかいていく。

今度は半径1から始まって次の半径は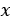 ,次の半径は
,次の半径は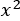 ,その次の半径は
,その次の半径は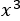 と半径が大きくなっていく長方形を考える。
と半径が大きくなっていく長方形を考える。
しかし先の長方形もそうであるが,この半径の変化は滑らかでない。次のようなグラフである。
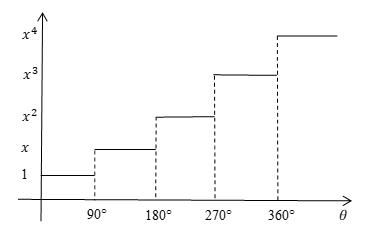
そこで,これを滑らかにするために,360°での 4 乗だから,90°で1乗。
よって1°では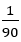 乗。よってθ°では
乗。よってθ°では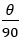 乗と考える。
乗と考える。
すると角度がθ°のときの半径は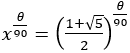 である。
である。
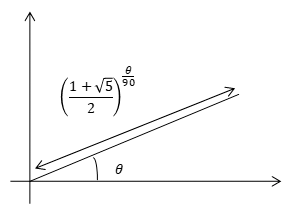

半径を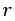 とすれば
とすれば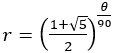 と表せる(ただし度数法で)。
と表せる(ただし度数法で)。
これはθ方向の原点からの距離を表す。
弧度法では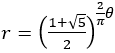 と表される。これをもとに曲線をかくと次のようになる。
と表される。これをもとに曲線をかくと次のようになる。
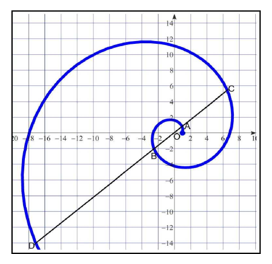
数学では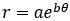 と表せる曲線のことを「対数螺旋」とよぶ。
と表せる曲線のことを「対数螺旋」とよぶ。

この場合,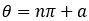 のとき,
のとき,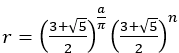 と計算でき,原点を通るいかなる直線で切っても,切り口は相似になる。
と計算でき,原点を通るいかなる直線で切っても,切り口は相似になる。
つまり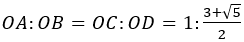 となる。
となる。
ちなみに,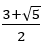 は黄金比の2乗で,「第2黄金比」とよばれる。
は黄金比の2乗で,「第2黄金比」とよばれる。
オウムガイの殻はこの曲線に近い。自然界の動物の行動でも観察される。例えば,隼(はやぶさ)が獲物に近付くとき,対数螺旋をかいて飛行する。その理由は,獲物を一定の角度で視認するためと考えられる。同様に,蜂が花に向かって飛ぶ軌跡も対数螺旋に近い。
この場合図の中心からのOPと接線との角∠OPTを計算すると,∠OPT≒72.97°である。
曲線状どの点でもこの角は一定であり,「等角螺旋」ともよばれている。(証明は数学Ⅲの微分を使う)隼は獲物を約20°ほど右に見ながら旋回していることになる。
今度は,黄金比以外の長方形を正方形で分割していくことを考えよう。黄金比の場合,正方形が1個ずつとれた。他の比の場合も考える。
まず縦横の比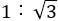 の長方形を考えてみる。この比は「プラチナ比」または「白金比」とよばれている。ちなみにこの長方形は,次の図にあるように,三つ折りにすると元の長方形に相似になる。(白銀比の場合は2つ折りで相似であった。)
の長方形を考えてみる。この比は「プラチナ比」または「白金比」とよばれている。ちなみにこの長方形は,次の図にあるように,三つ折りにすると元の長方形に相似になる。(白銀比の場合は2つ折りで相似であった。)
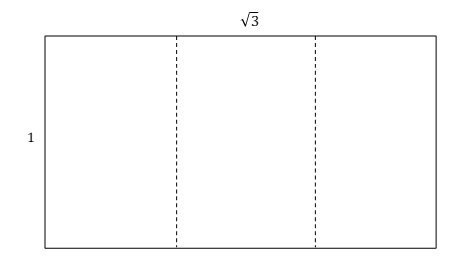
この長方形から正方形をとっていく。
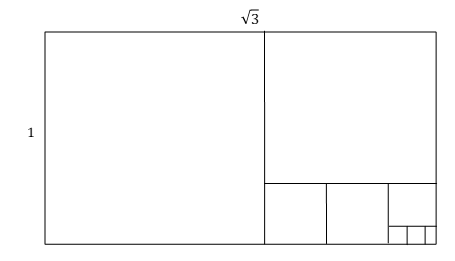
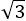 =1.732・・・より一辺が1の正方形を1つとることができる。残った長方形は
=1.732・・・より一辺が1の正方形を1つとることができる。残った長方形は
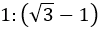 の長方形である。ここからいくつの正方形がとれるかが問題であるが,
の長方形である。ここからいくつの正方形がとれるかが問題であるが,
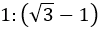 を
を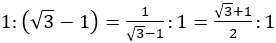 と変形し,
と変形し,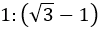 の長方形の代わりに元の長方形と相似な
の長方形の代わりに元の長方形と相似な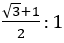 の長方形で考える(次図)。
の長方形で考える(次図)。

まず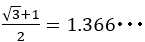 であるので正方形は1つとれる。残った長方形は
であるので正方形は1つとれる。残った長方形は
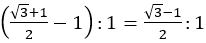 の長方形である。
の長方形である。
そしてこの長方形から正方形がいくつとれるかが問題になる。前と同じように比を
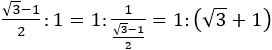 と変形し,
と変形し,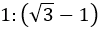 の長方形で考える。
の長方形で考える。
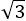 +1=2.732・・・であるので,正方形は2つとれる。残った長方形は,
+1=2.732・・・であるので,正方形は2つとれる。残った長方形は,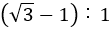 の長方形であり,これは最初に正方形を
の長方形であり,これは最初に正方形を
1つ切り取った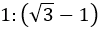 の長方形と実質同じものになって繰り返すことになる。
の長方形と実質同じものになって繰り返すことになる。
つまりこの後,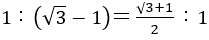 と変形し,1つの正方形がとれ
と変形し,1つの正方形がとれ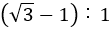 の長方形が現れ,残った長方形からは正方形が2つとれる。これが続く。
の長方形が現れ,残った長方形からは正方形が2つとれる。これが続く。
結果として1: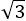 の長方形は正方形が順に1つ,1つ,2つ,1つ ,2つ,1つ・・・ととれる。これを[1,1,2,1,2,1・・・] とかくことにする。
の長方形は正方形が順に1つ,1つ,2つ,1つ ,2つ,1つ・・・ととれる。これを[1,1,2,1,2,1・・・] とかくことにする。
計算のアルゴリズムは単純である。そしてここから出てくる整数が正方形のとれる個数である。
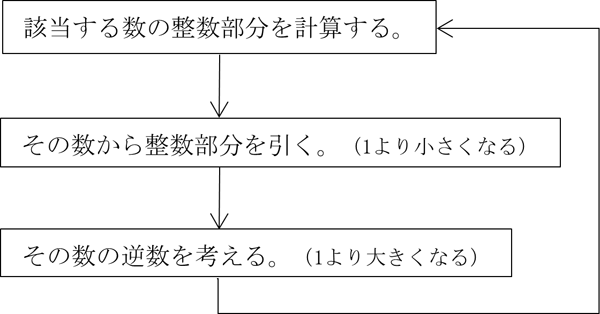
この流れを1つの式で表してみる。 の値を変えないで,そのまま変形する。
の値を変えないで,そのまま変形する。
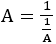 と変形するのが鍵である。
と変形するのが鍵である。
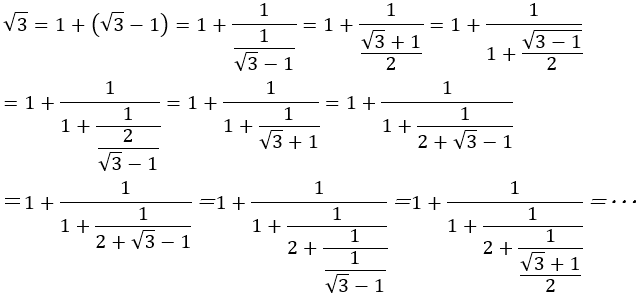
このように表された分数を「連分数」という。そして各分数の左側に現れる整数が,正方形がとれる個数である。
有理数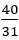 の場合はどうであろうか。
の場合はどうであろうか。
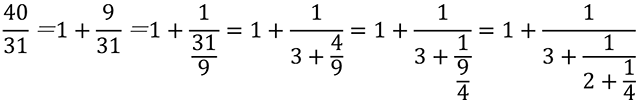
上式の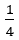 のように,分子が1になったらそこで終わる。この場合正方形は,1個,3個,2個,4個とれて終わりである。[1,3,2,4]とかける。
のように,分子が1になったらそこで終わる。この場合正方形は,1個,3個,2個,4個とれて終わりである。[1,3,2,4]とかける。
このように有理数の場合は有限の処理でストップする。しかし無理数の場合は,無限に続き,中には循環することがある。
改めて黄金比について,連分数から考察する。
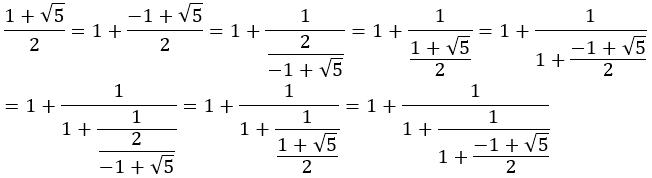
黄金比の場合には[1,1,1,1・・・]と続き,一番単純であることがわかる。これは2次方程式から次のようにも説明できる。
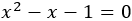 から
から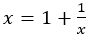
よって,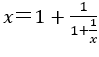 さらに,
さらに, と続く。
と続く。
連分数で出てくる式にx=1を代入してみる。すると,そこにはフィボナッチの数列の前後の比がでてくる。
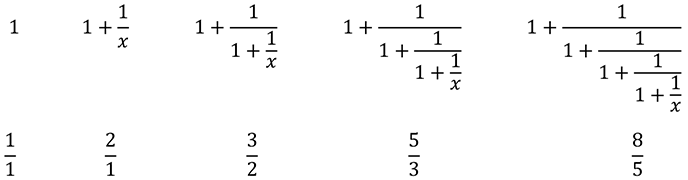
前述した一番小さい長方形(黄金比の長方形)を面積1の正方形に近似したとき,長方形の各辺がフィボナッチ数列になったこと(右図)を,ここでは式で説明したことになる。
ところで,連分数による表示は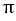 等,変形が困難な数に対しても行うことができる。
等,変形が困難な数に対しても行うことができる。
ただし,その数の値がある程度わかっている必要がある。
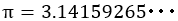
上記の精度でわかれば,電卓である程度計算していくことができる。
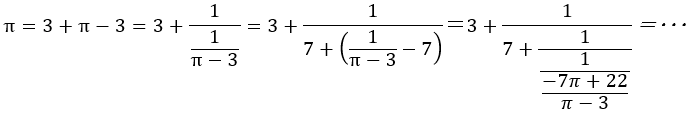
以下計算を続けていくと,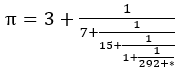
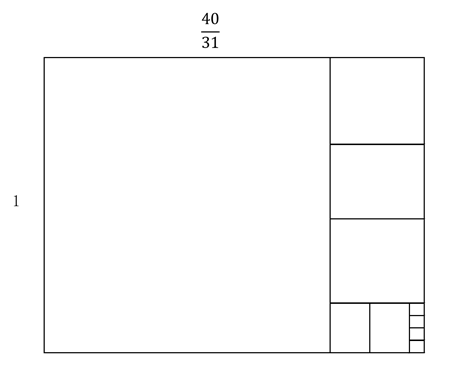
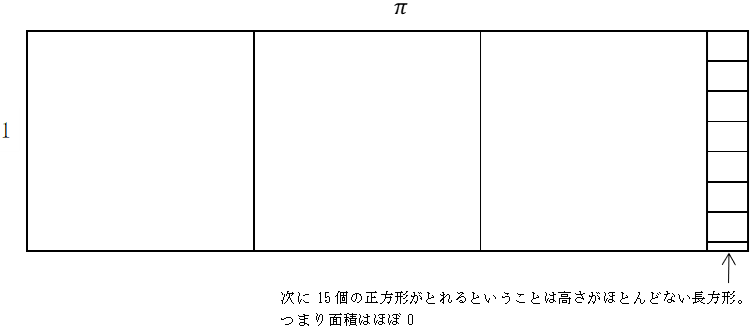
計算の途中,整数部分が今までになく大きい値がでることがわかる。この場合15や292がそうである。整数が大きいとき,
たとえばこの場合なら

は0に十分近くなり,この値を0にしてもある程度の精度をもった近似ができるはずである。実際これらを0として計算すると,次のようになる。分母が小さい割に,かなりの精度での近似である。下図はそれを図で表している。

一般に連分数の計算で,大きな整数が出る一歩手前で計算をやめると,精度が高い分数近似が得られる。
下図はそれを表している。
ところで次のような近似をすれば,どんな無理数も分数の近似ができる。しかし分母をかなり大きくしなければならない。
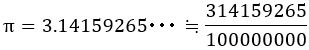
連分数による近似は,分母を大きくしないで無理数の近似を行うことができる方法である。
ところで,黄金比の場合はどうであろうか。出てくる整数はすべて1である。もちろん下の連分数の計算で「*=0」とすることで近似はできる。でてくる分数はフィボナッチ数列の前後の比である。しかし,その近似はπの場合と比べて緩慢であり,くじに当たったような分母が小さい割に精度が高い近似はない。繰り返し述べるが黄金比も分母を大きくすれば近似精度の高い分数はある。しかし分母が小さい分数でラッキーな近似ができる分数はないのである。

連分数ででてくる整数の大小をみれば,その数に近い分数でラッキーな分数がどのくらいあるかわかり,次のことがいえる。
黄金比に近い分数は無数に存在する。分母を大きくすれば,黄金比とその分数の差はいくらでも小さくなる。しかしすべての数の中で,黄金比が一番分数を寄せ付けない数である。その意味で,有理数から一番離れている。これについては,(15)以降さらに数学的に示していく。
19世紀から20世紀にかけて,無理数の周りの有理数の分布について様々な研究がなされた。
例えば,連分数で整数が順番に1,2,3,・・・ n,・・・とでる無理数は,整数の上限がなく,有理数にかなり近い数といえる。
実は黄金比の有理数を寄せ付けないこの性質が,自然界の中に黄金比が多く存在する原因の1つである。
ここでは,植物が葉を出していく際に,黄金比がどのように関係するかについて,VB でつくったシミュレーションするプログラムから説明することにする。
〇=葉に見立てて植物が葉を出していく様を上からかいてみる。 円(葉)の半径は1。
円(葉)を一定の角度回転( 回転)させて
回転)させて 枚目の葉の中心(茎)からの距離は
枚目の葉の中心(茎)からの距離は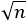 と考える。なぜこのように考えるかというと,半径が
と考える。なぜこのように考えるかというと,半径が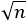 の円の面積は
の円の面積は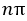 である。
である。
一方円に見立てた1枚の葉は面積πである。これが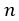 枚あるので葉の面積計は大円の面積
枚あるので葉の面積計は大円の面積 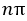 に等しいのである。理想的には重なりなくちょうど葉を配置できるが,葉の形状が円であることを考えると多少の重なりはやむを得ない。
に等しいのである。理想的には重なりなくちょうど葉を配置できるが,葉の形状が円であることを考えると多少の重なりはやむを得ない。
また は
は =1で360°の意味である。当然,円(葉)の重なりの部分が少ない程,太陽の光を浴びることができ,光合成ができる。円200枚でシミュレーションした。
=1で360°の意味である。当然,円(葉)の重なりの部分が少ない程,太陽の光を浴びることができ,光合成ができる。円200枚でシミュレーションした。
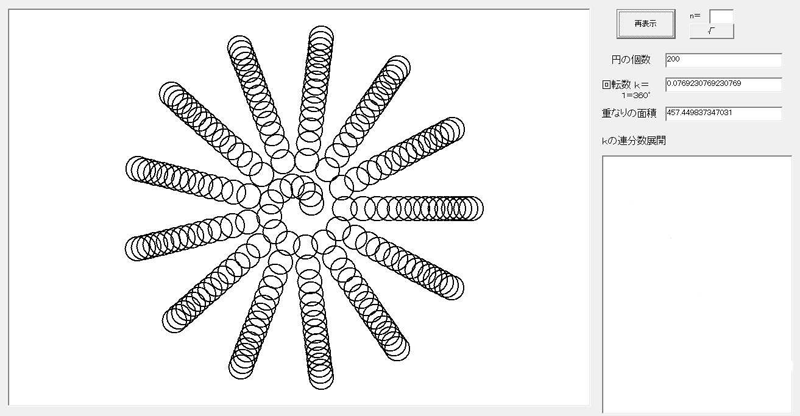
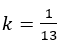 重なりの面積和=457
重なりの面積和=457
この場合放射状になり,葉は重なってしまうことがわかる。分数の場合はこのように放射状になる。これは のように,分子が1でなくても(分子に関係なく)起こる。
のように,分子が1でなくても(分子に関係なく)起こる。
ただし,分母が大きくなると,次のように螺旋のような模様になることもある。
 =0.717171717171 重なりの面積和=139
=0.717171717171 重なりの面積和=139

この場合なら連分数の整数のところで,「6」が現れる。この前で展開をやめて分数にすると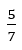 である。0.7171・・・≒
である。0.7171・・・≒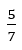 であることがわかる。しかし真に等しければ放射状になるが,わずかに値が違うので斜めにずれる。それが7本の螺旋になっているのである。
であることがわかる。しかし真に等しければ放射状になるが,わずかに値が違うので斜めにずれる。それが7本の螺旋になっているのである。
しかも0.7171・・・の方がわずかに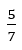 より大きいので左回りの螺旋になる。葉の数を増やしていくと,0.7171・・・=
より大きいので左回りの螺旋になる。葉の数を増やしていくと,0.7171・・・=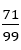 なので,
なので,
99本の螺旋が現れる。
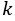 =
=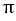 重なりの面積和=440
重なりの面積和=440

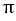 の場合,連分数で整数で15が現れる。前述したようにその前でやめると,
の場合,連分数で整数で15が現れる。前述したようにその前でやめると,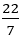 なので,7本の螺旋が現れる。しかしこの後,連分数の整数には292が現れ,その前でやめて計算すると,
なので,7本の螺旋が現れる。しかしこの後,連分数の整数には292が現れ,その前でやめて計算すると,
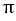 ≒
≒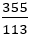
となる。この後1万枚の葉を並べると,次のようになり,113本の枝が現れる。
この場合,近似の精度が非常によいので,113本の枝は曲がらずに外側に伸びている。

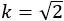 重なりの面積和=69
重なりの面積和=69
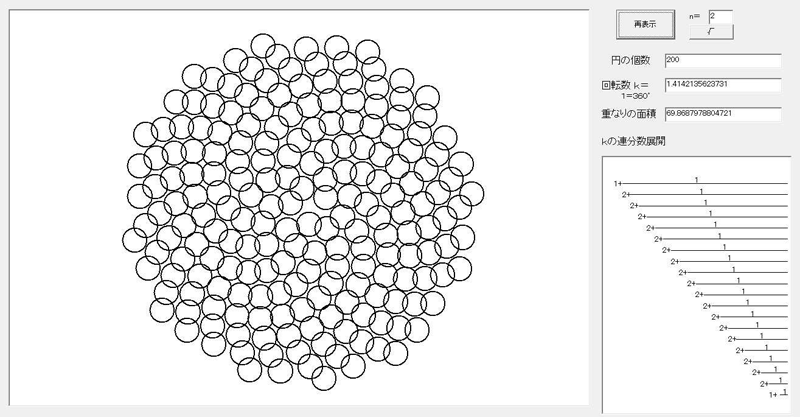
この場合,連分数の整数はすべて2である。そんなに大きな値ではない。ラッキーな近似できる分数もない。螺旋もそれほど見えないし,重なりも少ないことがわかる。
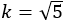 重なりの面積和=145
重なりの面積和=145

この場合は連分数の整数はほとんど4である。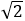 に比べると,螺旋ができて重なりは多くなる。
に比べると,螺旋ができて重なりは多くなる。
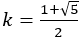 重なりの面積和=48
重なりの面積和=48
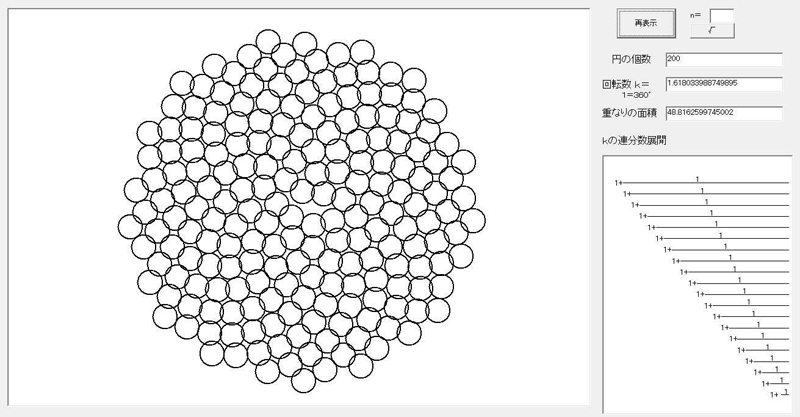
最後に黄金比の登場である。
連分数で整数はすべて1。一番葉の重なりは少ない。光合成にとっては都合がよい。
この黄金比の回転角は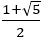 =1.618034回転なので度数法で左周りで222.49°,
右回りで137.51°である。
=1.618034回転なので度数法で左周りで222.49°,
右回りで137.51°である。
この角のことを「黄金角」という。もちろん,黄金角の回転の場合も螺旋ができる。どんな螺旋であろうか。
黄金比がフィボナッチ数列の前後の比と近似している。自然界にはこれらの数の分母の本数の螺旋がみられることがある。このうち,黄金比より少し小さい分数の分母5,13,34・・・は右旋回の螺旋,黄金比より少し大きい分数の分母は3,8,21・・・は左旋回の螺旋になることが多い。
このことを説明するには植物の葉や花や種になる生殖細胞「原基」について言及しなければならない。この原基は茎の中心部分にあるが,花や種の細胞になっていくにつれ,外側に押し出されていく。その間も花や種の細胞となる原基は中心部分から生まれ続けている。従って,外側にある花や種は最初に出来たものであり,中心に近いところは後から出来たものである。従って時間とともに外側に新しい花や種が出来ていくのではなく,むしろ外側から中心部分に新しい花や種が出来ていく。しかも時計(右)回りに黄金比の回転をしながら新しいものが内側にできることが多い。
もし,ちょうど分数の分だけ回転すれば,たとえば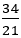 回転したとすれば,中心から放射線状に21本の枝ができるわけだが,黄金比の方がより少し小さいので,次に出来た新しい種が内側に並ぶとき,直線ではなく,回転が少し足らない状態で並んでいく。
回転したとすれば,中心から放射線状に21本の枝ができるわけだが,黄金比の方がより少し小さいので,次に出来た新しい種が内側に並ぶとき,直線ではなく,回転が少し足らない状態で並んでいく。
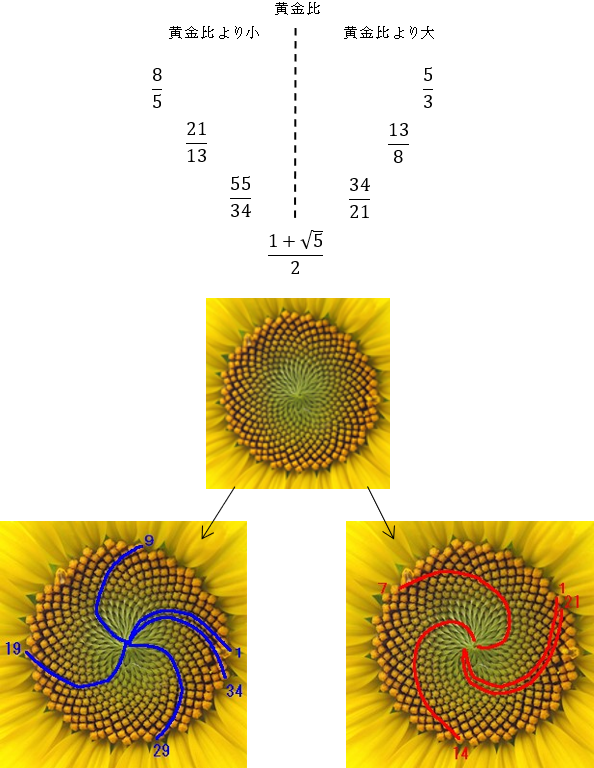
結果34本の螺旋は中心から右に旋回する曲線になる。
またちょうど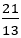 回転した場合は中心から放射状に21本の枝ができる。しかし黄金比の方が
回転した場合は中心から放射状に21本の枝ができる。しかし黄金比の方が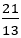 より少し大きいので,回転が少しオーバー気味に内側に並ぶ。結果,21本の螺旋は中心から左に旋回する曲線になる。
より少し大きいので,回転が少しオーバー気味に内側に並ぶ。結果,21本の螺旋は中心から左に旋回する曲線になる。
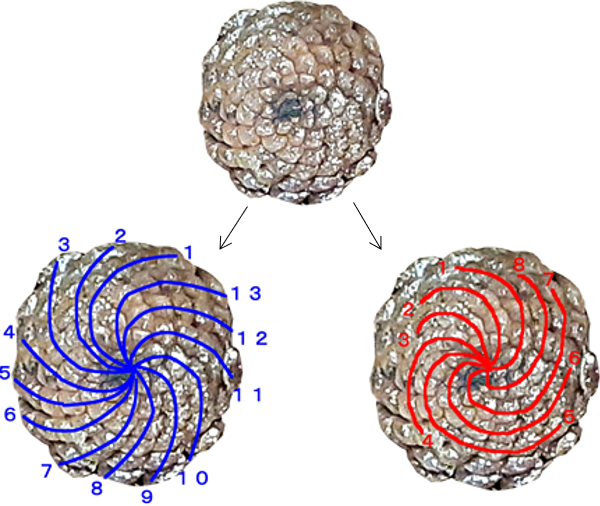
松ぼっくりにも黄金比が現れる。下図のように螺旋の本数に8や13が現れ,これはフィボナッチの数列の一部である。
ただ,前述したように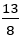 より黄金比はやや小さく,
より黄金比はやや小さく,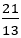 よりも黄金比はやや大きい。従って13本の螺旋は右に旋回し,21本に旋回する曲線になる。
よりも黄金比はやや大きい。従って13本の螺旋は右に旋回し,21本に旋回する曲線になる。
さて後編では黄金比のほかに白銀比や青銅比についても言及し,黄金比の存在について数学的に再考する。