
私の実践・私の工夫(算数)
子どもが発展的に考えていくことを大切にした単元構成
~「合同な図形」~
5年

1.自然な思考の筋を大切に
図形の概念形成を考えるにあたって,わたしたちは,日頃どのように思考して概念を形成しているのかをまず考えたい。例えば,これから初めてお会いすることになる外国の方の人物像についてはどうだろうか。はじめにわたしたちは,その人の名前や性別,出身国や外見などの情報を手がかりとして「たぶん,こんな方じゃないかな。」と推測しているのではないだろうか。そして,実際にお会いする中で新しく得られた情報をもとに,推測したことを組み直しながら,その方の人物像を形成していると思われる。
このようにわたしたちが自然に働かせている思考の筋を,子どもが合同な図形を調べていく際も大切にしたい。そこで,本実践では,子どもにとって手がかりとなるものが多い図形から取り組んでいくようにしたいと考えたところである。
2.単元構成について
子どもにとって手がかりの多い図形とは何であろうか。それは以前から慣れ親しんでいる図形であると考える。例えば,小学校入学以前にも,子どもたちは折り紙遊びなどの経験を通して,正方形の全ての辺の長さは同じであることを感覚的につかんできていると思われる。また,あやとり遊びなどを通して,閉曲線が様々な形に連続的に変化する様子を見てきたかもしれない。そして,小学校入学後は,算数の授業の中で,操作を通して図形の理解の基礎となる経験を増やしながら,図形の構成要素や要素間の関係に目を付けて図形を分析的に見る学習経験を積んできている。
このようなこれまでの生活経験,学習経験から,5年生の子どもにとって考える手がかりの多い図形とは,平面図形の中でも「正方形」「長方形」「正三角形」「平行四辺形」など,名前の付いている図形であるととらえる。これらの図形について,子どもは「全ての辺が同じ長さ」「全ての角が直角」「向かい合った辺が平行」などとつかんできている。本単元において,合同な図形についての観察や構成を通して,平面図形の理解を一層深めることができるような学びを展開していきたい。
このようなことから単元の構成を次のように考えた。
Ⅰ ジオボードで図形を構成する。(長方形や正方形,二等辺三角形など 子どもの問い 「図形は,何で決まるのかな。」 Ⅱ 紙上に合同な三角形を構成しながら,図形が決まることについて探る。
3.授業の実際
図形は,何で決まるのかな ~ジオボードで合同な図形をつくろう~
単元のはじめに,透明なジオボードで合同な長方形をつくる活動に取り組んだ。透明なので,子どもは自分がつくった図形を他の人がつくった図形と直接重ねて比べることができる。子どもは自分のつくった形が同じかどうか,周りの子とボードを重ね合わせて確かめていた。そして,何度かつくる中で次のような話になっていった。

「長方形は,よことたてだけで形が決まるよ。」
「正方形は,最初にひっかけた2つの頂点(一辺)だけで決まるね。」
子どもは,これまでに学んできたことについて,ジオボードで図形を構成する活動を通して,正方形,長方形,平行四辺形,ひし形は,合同な三角形が2つで構成されている図形であるが,その点において台形は少々異なるということにも気付いていった。
正三角形の頂点Aの位置は,何で決まるのかな。

合同な四角形について問題解決が一段落したので,合同な三角形について調べていくことになった。その中で,ジオボードでは,二等辺三角形はできるが,正三角形ができないということがはっきりした。その際,子どもから,「でも…,ノートにだったらかけるんじゃないかな。」というアイディアが出てきた。そこで,皆でノートに正三角形をかきながら調べていくことにした。
この活動に関連する前学年までの主な学習内容として次のものがある。

・第3学年…辺の長さが全て等しい
・第4学年…角の大きさが全て等しい(60°)
子どもは,これらの知識を活用しながら,たくさんの方法を考えていった。そして,考えた方法に名前を付けながら,表にして整理していった。
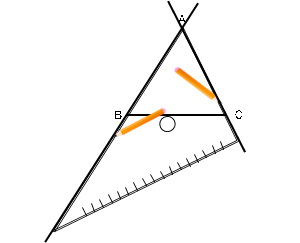
様々な方法を考える中で,A児から,
「三角定規の60°のを使うんですけれど…。」
と新たな方法が出された。右図のように底辺BCと頂角Aを使う方法である。それを聞いた子どもたちが,
「この三角定規は,どこにあわせるの?」
「これは,かけないんじゃないかな。」
「いや…真ん中にあわせれば…。」
などと次々につぶやきはじめ,ノートにかいて確かめ始めた。
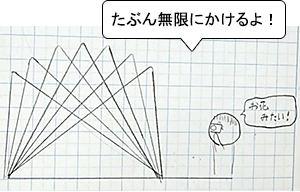
すると,今度は教室のあちらこちらから,
「こんなところにもかける!」
「お花みたい。(右写真:子どものノート)」
という話になった。そこで教師が,
「じゃあ,おもしろいけれど,この方法では正三角形の頂点Aは決まらないということかな。」
と話すと,一瞬静寂が訪れたが,B児がすっと手を挙げて話し始めた。
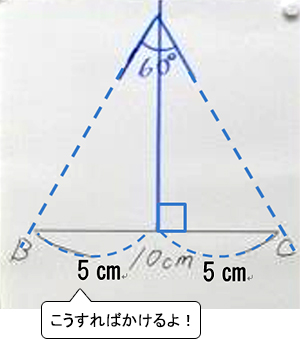
「でも…,正三角形は,頂点Aが真上にあるから,辺BCの中心の線(底辺の垂直二等分線)に合わせればかけるんじゃないかな。」
実際に右図のようにしてかいてみると,確かに合同な正三角形がかけることが分かり,拍手がおこる。A児もB児もとても嬉しそうである。この方法を子どもたちは「中心法+上角法」と名付けた。
そして,二等辺三角形は,ここまで考えてきたかき方でかけるので,別の三角形で確かめていきたいということになり,次に直角三角形の頂点Aは,何で決まるのかを調べていくことになった。
直角三角形の頂点Aの位置は,何で決まるのかな。
はじめに,どのように取り組んでいこうとしているのかを確認した。すると,「正三角形で考えた方法を一つ一つ試していったらいいんじゃないかな。」と出てきて皆が賛同する。三辺の長さを使ってかく方法から試していく。
すると,すぐに「できる。」と皆が納得した。そこで,次に中心の線を生かしてかく方法を試していくことになった。C児が「これは無理なんじゃない…。」とつぶやいている。指名すると,「直角三角形は,頂点Aが中心からずれているからかけないと思う。」と述べ,皆で確かめていった。その中で,「でも…直角二等辺三角形は決まるんじゃない。」とD児がつぶやき,皆で「おお!」と感動しながら直角三角形の例外も確認することができた。角度を生かした方法は「決まった。」とすぐに皆で納得した。
そのようにしながら,全ての種類の三角形に通ずる方法を見出しながら,子どもは,「図形は,頂点がどこに決まるかで決まる」ととらえていった。
4.これからの単元づくりに生かしたいこと
・単元の導入で,子どもは,これまで慣れ親しんできた図形をジオボードで構成し,子どもはゴムをかける場所(頂点)の位置によって図形が連続的に変化していく様子を目の当たりにしてきた。そのことで,単元中盤以降で,子どもがノートにかいた静的な図形を手がかりに考える際にも,頂点の位置に伴う辺の長さや角度の変化が動的に見え,発想の源泉になっていたと思われる。
・正方形・長方形→平行四辺形→台形,正三角形→直角三角形→三角形と,特殊から一般の流れで単元を展開した。そのため,子どもは手がかりとなる既知の情報をもとにしながら具体的に考えることができた。一つが明らかになることで「じゃあ,別の三角形では?」と考えていく姿勢がみられた。これからも子どもにとって学習活動の連続性や意味がある単元づくりに取り組みながら,子ども自身が発展的に考え,一般化していこうとすることを大切にしたい。


