 問題は、分かるか、分からないかではなく
問題は、分かるか、分からないかではなく
考え方や、ものの見方を理解できるか。
さて、あなたはどう考えましたか?
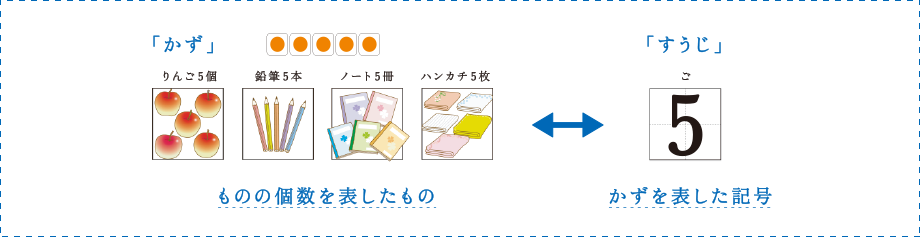
「かず」と「すうじ」
「スーパーマーケットの駐車場に,車が35台とまっています」といったとき,この35台は「かず」ですか,「すうじ」ですか?
「35台」は車の台数をしめすかずで,
3と5を使った「35」は,「35をつくるすうじ」です。
このように,数が2けた以上になると分かりやすいですね。
かずとすうじの区別は,1けたになると区別がつきにくくなります。
例えば,「コップを5個並べてね」と話したときと,「ノートに5を書いてみよう」といったときの「5」は,同じように見えても違います。
「コップ5個」の5個はコップのかずを表し,「ノートに書いた5」の5は5というすうじです。
かずは,りんご5個,鉛筆5本,ノート5冊のように,ものの個数を表したものです。
「かず」の役目
かずには,基本的に2つの役目があります。
1つは,ものの多さを表すために使う役目
もう1つは,ものの順番を表すために使う役目です。
「駐車場に車が5台とまっています」というときの5と
「私の車は左から5台目です」というときの5は,表していることが少し違います。
「駐車場に車が5台」の5台は,とまっている車の多さ(台数)を表し,「左から数えて5番目」の5番目は,
多さでなく順番を表しているからです。
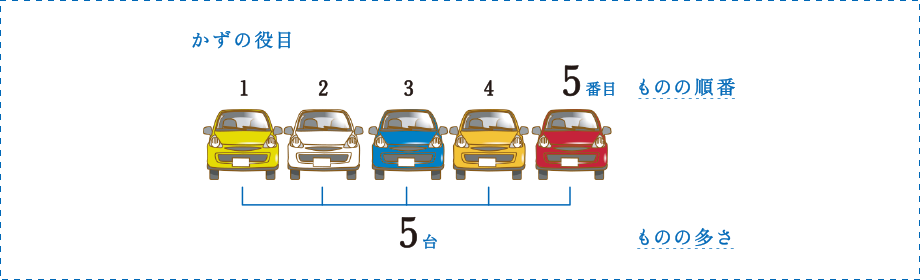
このように,かずには多さ(大きさ)を表すかずと,順番を表すかずがあります。順番を表すかずは,多さや大きさでなく,位置や時間からかぞえて何番目かを表すために使われるかずなのです。
無限の「かず」,いろいろな「すうじ」
かずの大きさには限りがありません。どんな大きなかずでも,そのかずに1をたすと,もっと大きなかずになるからです。これは別の言葉で「かずは無限にある」ということにほかなりません。
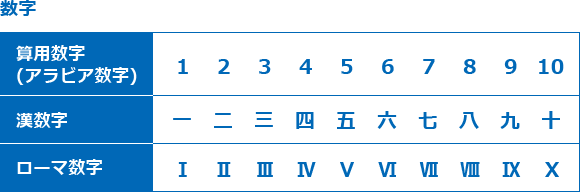
すうじは,「0,1,2,3,4,5,6, 7, 8, 9」という10個の文字を使ってかずを表した記号です。この10個の文字を算用数字,またはアラビア数字といいます。
そのほか,日本では漢字でかずを表し,昔のローマではローマ数字という文字でかずを表しました。
歴史的には地域によって異なるすうじを使っていたこともありますが,今日,算用数字として使われるすうじは全世界共通です。
さらに、こんな問題も考えてみましょう。
単位の計算
例えば,今日があなたの10歳の誕生日だとすると
あなたは生まれてから10年経ったことになります。
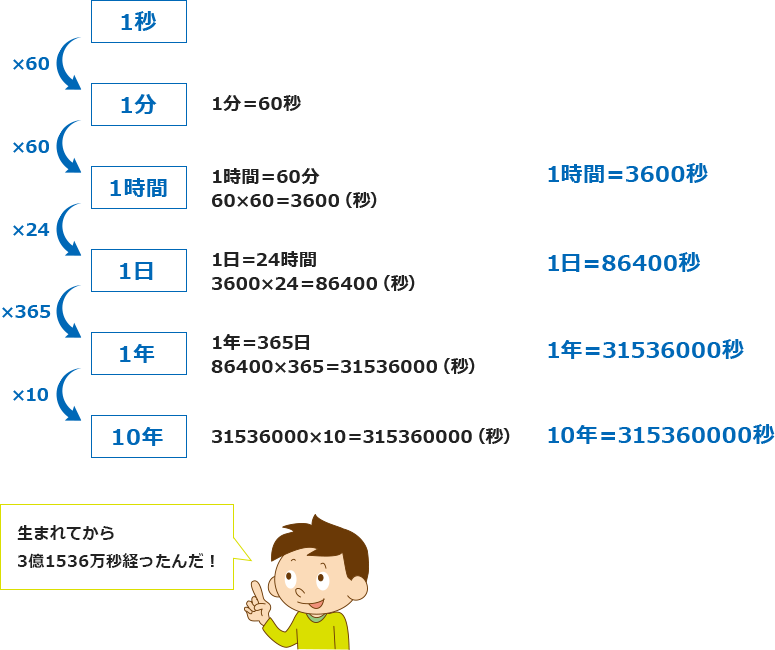
10年が何秒になるかを,次の方法で計算しましょう。
方法
1分=60秒,1時間=60分,1日=24時間,1年=365日の
関係から,10年を秒になおす。
「うるう年」の計算
ここまで計算して,「うるう年」を入れていなかったことに気が付きましたか?
1年の長さは,地球が太陽の周りを1周するのにかかる時間ですが, 365日ちょうどでなく,365.2422日(365日5時間48分46秒)かかります。そこで,4年に1度,「2月29日」を入れて,地球の進み方に暦を合わせているのが「うるう年」です。
ところが,うるう年を重ねると,今度は,地球が1周する時間より暦の1年間のほうが長くなってしまいます。このずれを修正するため,400年に3回,うるう年が減らされています。
うるう年の決め方
- 西暦が4で割り切れる年は,うるう年。
例 2008年,2012年,2016年,2020年など - ①の例外として,西暦が100で割り切れ,400で割り切れない年は,うるう年としない。
例 1900年,2100年,2200年など

素数とは?
素数とは,どのような数でしょう。
例えば,18は,9×2,6×3,3×3×2
と,かけ算で分けることができます(どんな数でもその数×1で表せますが,その数×1は,かけ算で分けたとはいわないことにします)。
このうち,3×3×2は,これ以上,小さい数のかけ算に分けることができません。
1から10までの数を上のようなかけ算で考えてみたとき,
かけ算に分けられる数と,分けられない数があることがわかります。
2,3,5,7のように,かけ算で分けられない数を素数といいます。
素数は,「1とその数でしか割り切れない数」という言い方をします(素数に1は含みません)。
2以上の数は,必ず,素数か素数でない数のどちらかになります。
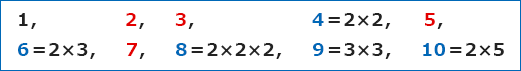
素数を探そう
紀元前3世紀,素数に興味をもったギリシャ人のエラトステネスは,素数の探し方として,「ふるい」の考えを用いました。
ふるいとは,粉や砂などの細かいものを網目を通して落とし,より分ける道具のことです。

エラトステネスは,2,3,5,7,…という素数の倍数を除いていって,残ったものを素数としたのです。
このように,数を一つひとつ,落ちなくしらみつぶしにつぶしていく方法は,現代のコンピュータでも,使われています。
エラトステネスのふるい
100以下の素数を,次のようにして見つけましょう。

残った数をすべて書くと,下の25個の数が,100以下の素数です。
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
円の面積の公式を,自分でつくってみましょう。
円の面積を,2通りの方法で求めてみましょう。
方法1 ひもを使って考える。
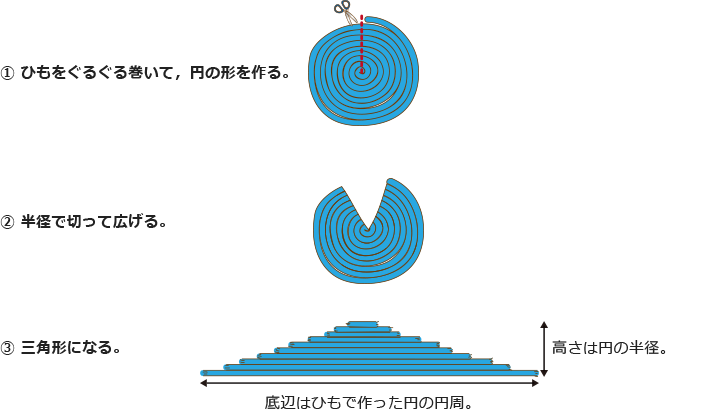
円が三角形になりました。だから,
三角形の面積=底辺×高さ÷2 より,円の面積は次の式で求められます。

円周は(直径×円周率)で表せるので
円の面積=円周×半径÷2
=直径×円周率×半径÷2 (直径÷2は半径だから)
=半径×円周率×半径
=半径×半径×円周率
方法2 円をおうぎ形に細かく等分して考える。
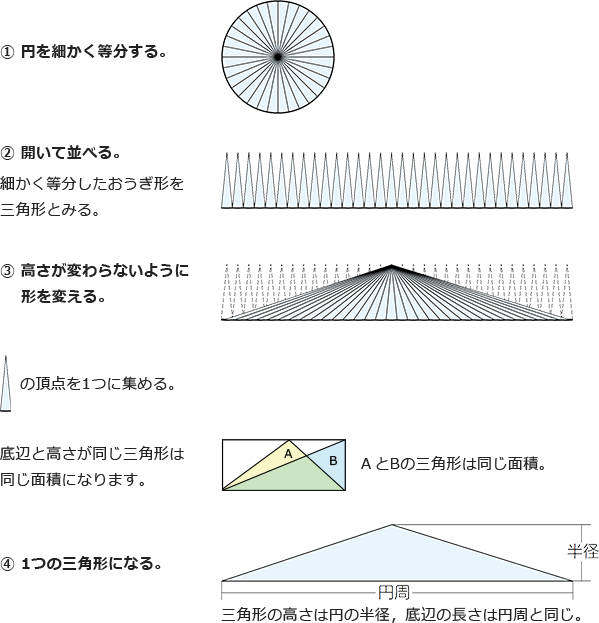
三角形の面積=底辺×高さ÷2 より,円の面積は次の式で求められます。

方法2でも,方法1と同じように,「円の面積=半径×半径×円周率」という,見慣れた式をつくることができます。