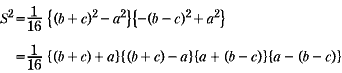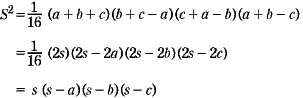数学トピックQ&A
 数学目次へ
三角形の面積
Q 　△ABC の面積 S は で与えられるというのは，三角形の（2）2辺角の場合の公式ですが，（1）3辺（3）2角辺の場合に相当する公式はあるのですか。
A 　三角形の形状について，（1）（3）の場合も残りのものが決まることを発展のところで確かめたので，面積を表す式もありそうです。
（1）3辺の場合には，有名なアレクサンドリアのヘロン（Heron 紀元60年頃）の公式があります。
　　として，
Q 　こんな古い時代に，すごい式を見つけたものですね。
A 　測量には便利な式ですね。
　では，これを証明してみましょう。
　　……[1]
　[1] の両辺を2乗して，を使うと，
　　……[2]
となります。
　余弦定理　 を[2]に代入すると，S は a，b，c の式になります。
まず，[2]で，としておいて，計算してみましょう。
Q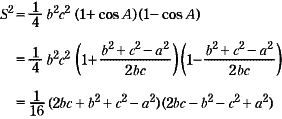 　　

となりました。
A 　b2＋c2＋2bc，b2＋c2−2bc は因数分解できます。

　　

これに[1]の2s＝a＋b＋c を代入するとどうなりますか。
Q 　a＋b＋c ＝2s，a＋b＝2s−c ，b＋c ＝2s−a，c ＋a＝2s−b だから，

　　

よって，
　　この公式は，形がきれいで，覚えやすいですね。
A 　ご苦労様でした。
　（3）2角辺の場合は，a，B，C が与えられたとして，面積を求めてみましょう。
　……[1]　で，b，c を a，B，C で表せばよい。
　正弦定理から，
　これを[1]に代入するとどうなりますか。
Q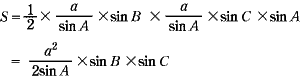 　　
A 　A＋B＋C＝180°だから，

　　

　これを使うとどのようになりますか。　
Q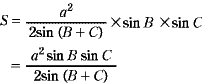 　　

となります。
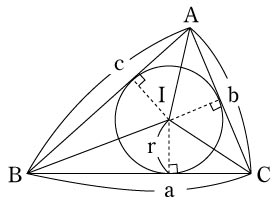
A 　これで，すべてが解決されたことになります。
　　三角形の面積は，古くからいろんな公式が知られています。内接円の半径 r や外接円の半径 R を使って表す公式もあります。
　ア　内接円の半径 r と3辺の長さ a，b，c で表す。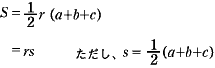
　　　

　イ　外接円の半径 R と3辺の長さa，b，c で表す。
　　　
　　　外接円の半径 R と3つの角 A，B，C で表す。
　　　S＝2R 2 sinA sinB sinC
　ウ　内接円の半径 r，外接円の半径 R，3つの角 A，B，C で表す。
　　　S＝Rr (sinA＋sinB＋sinC )
　いずれも，簡単ですから証明してみてください。
Q 　アは，△ABCの内接円の中心を I とすると，
　　S=△IBC＋△ICA＋△IABになっています。だから，
　　　
　イは， に，正弦定理 を代入すればよい。
　　下の方の式は，正弦定理 a ＝2R sinA，b ＝2R sinB を代入すればよい。
　ウは，に，正弦定理　 a ＝2R sinA，b ＝2R sinB ，
c ＝2R sinC を代入すればよい。