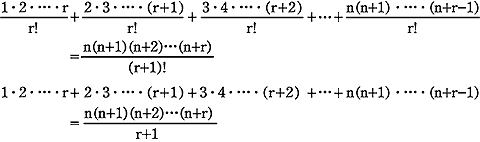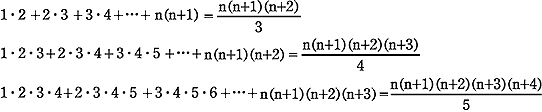1・2＋2・3＋3・4＋……＋n(n＋1)
　　　1・2・3＋2・3・4＋3・4・5＋……＋n(n＋1) (n＋2)
　　　1・2・3・4＋2・3・4・5＋3・4・5・6＋……＋n(n＋1) (n＋2) (n＋3)

　ここではこれらの和を連続整数の積和と呼ぶことにしよう．

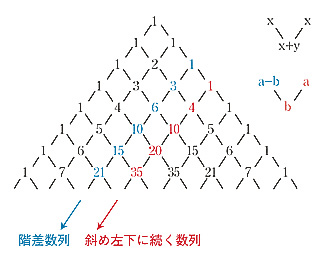
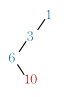
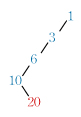
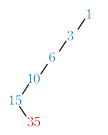
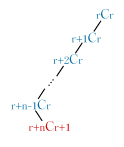
　これらの和の求め方は多くの参考書に書いてある．諸君のうちには知っている人も多いだろう．しかし，もっと簡単でわかりやすい解答があることを紹介しよう．
　実は，これらの解答はパスカルの三角形の中に隠されている．

　パスカルの三角形をよく見ると，次のように斜め左下に続く数列の階差数列（赤字）はその1段上の数列（青字）になっている．

したがって，

1＋3＝4	1＋3＋6＝10	1＋3＋6＋10＝20	1＋3＋6＋10＋15＝35

となっていることがわかる．

　これを一般化すると次の公式が成り立つ，

　左辺の級数の第 k 項は，

である．右辺の分子が k より始まる r 個の連続整数の積であることに着目しよう．

　こちらの分子は n から始まる r＋1個の連続整数の積である．
　よって，

とくに，次の等式が成り立つ．