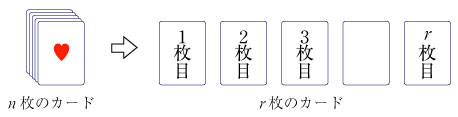
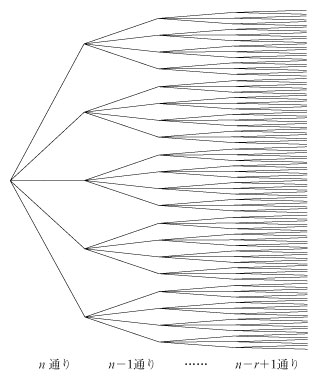
1．順列の個数 _nP_r（復習）

　まず、「n 個の異なるものから r 個を取り出すときの順列の数 _nP_r 」であるが、これは次のように求められる．
　例えば、n 枚のカードから r 枚のカードを取り出して並べることを考えてみよう．

　　1枚目のカード　　n　　 枚のカードから1枚を取り出す 　n　　　通り
　　2枚目のカード　　n−1 枚のカードから1枚を取り出す 　n−1 　通り
　　3枚目のカード　　n−2 枚のカードから1枚を取り出す 　n−2　 通り
　　……
　　r 枚目のカード 　n−r＋1枚のカードから1枚を取り出す 　n−r＋1通り

となるから、

　「r 枚を取り出して並べる」といったが計算をよく見ると、はじめに r 枚のカードの組合せを取り出しているわけではない．r 枚をいっぺんに取り出すのではなくて、じっさいは、1枚ずつ取り出すことを r 回くりかえしている．
　この計算を樹形図で表すと、形図ははじめ n またに分かれ、次に n−1 またに分かれ、…、最後に n−r＋1 またに分かれる．

2．組合せの個数 _nC_r　（復習）

　上で見たように、順列の個数は簡単に求められる．これに対し、組合せの個数は簡単には求められない．諸君はすでに教科書でこれを学んでいるはずだが、どうやって求めたかもう忘れているかもしれない．ここでもう一度これを見直しておこう．
　これを見直すことが次のステップへの足がかりとなる．

　例えば、1、2、3、4、5 と書いてある 5 枚のカードから 3 枚のカードの組を取り出すことを考えよう．

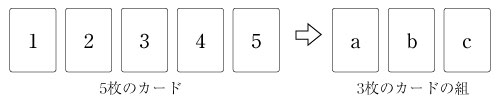
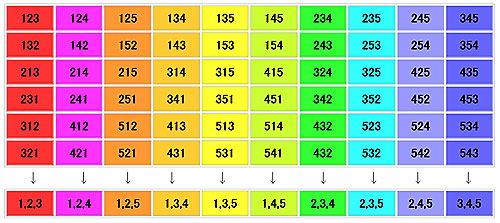
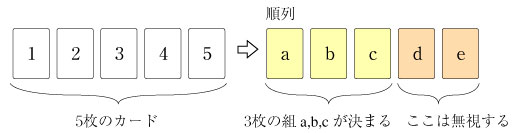
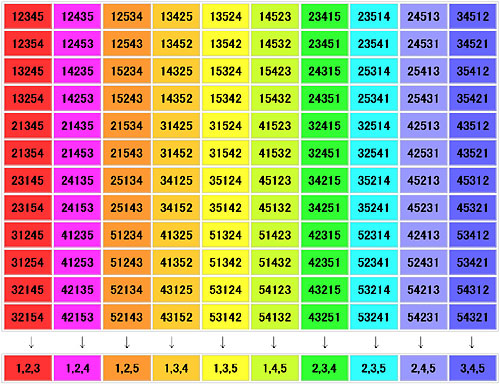
　そこで、3 枚のカードの組を手に入れるために、
　　　　　5 枚のカード　→　3 枚の順列　→　3 枚の組合せ
という方法を考える．
　この方法では同じカードの組合せが何通りもできる．
　この場合、3 枚のカードの順列は全部で ₅P₃＝60 通りあるが、下の図に見られるように、同じ組合せは 6 通りずつ得られる．

順列

組合せ

　例えば、1、2、3のカードの組合せは1、2、3の順列　123、132、213、231、312、321 から得られる．
　したがって、「5枚のカードから3枚のカードの組を取り出す」という場合の数は、

　₅C ₃

となる．

　一般に、n 個の異なるものから r 個のものを取り出す順列の個数は、
　　　
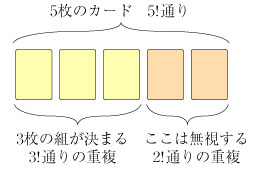
である．

3．組合せの個数 _nC_r　（別の見方）

　組合せの個数 _nC_r を入手するのに別の方法を考えよう．

　5 枚のカードから 3 枚のカードを入手する方法として、5 枚のカードすべての順列を考え、はじめの 3 枚が 3 枚の組を決めると考える．

　組合せの個数 ₅C ₃ は次のように決まると考える．

したがって、
　　　
となる．
　 _nC_r の公式
　　　
も同様に理解できよう．

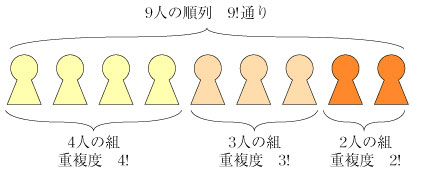
4．9人の人を4人、3人、2人の組に分ける

　ここまで書いたことのうち、1．と 2．はすでに知っていることの復習である．3．では組合せの個数について別の見方があることを示した．
3．の見方をさらに発展させて9人の人を4人、3人、2人の組に分ける問題を考えよう．
　9人の順列を次のように分割して組分けを入手することを考える．

　求める個数 N は、
　　　
である．
　一般に、n 人の人を A 組 p 人、B 組 q 人、C 組 r 人に組み分けするときの場合の数は、
　　　
となる．ただし、p＋q＋r ＝n とする．

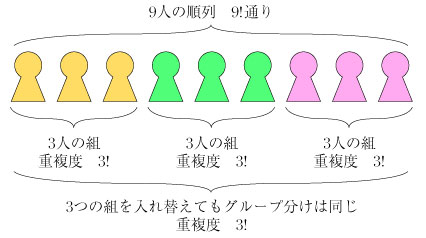
5．9人の人を3人ずつ3つのグループに分ける

　やはり、9人の順列を3人、3人、3人と分割してグループ分けを入手するが、組どうしの入れ替えが可能であることに着目する．

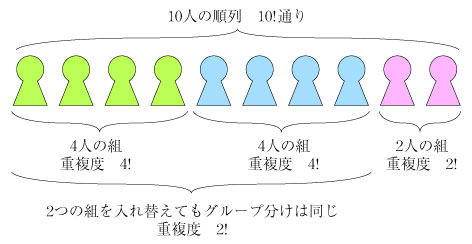
　求める個数 N は、
　　　
である．

　同様に、10人の人を4人、4人、2人のグループに分ける場合は，

と考えればよい．
　求める個数 N は、
　　　
となる．