| 偼偠傔偵
丂惗搆偑庼嬈偵嵟傕嫽枴傪帵偡偺偼丆悢妛揑敪尒偑偱偒偦偆偩偲姶偠偨弖娫偱偁傞丏栤戣傪敪尒偟偨応崌偼丆栤戣偑夝偗偨偲偒埲忋偵婌傃偼戝偒偄傛偆偱偁傞丏巹偺庼嬈偺幚慔椺傪枹敪昞偺傕偺偐傜丆僗働僢僠晽偵丆偄偔傜偐偁偘偰傒偨偄偲巚偆丏
1丏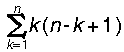
丂I孨偵巜柤偟偰傗傜偣傞偲丆掕愇捠傝偵夝傪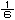 n(n+1)(n+2)偲弌偟偰偔傞丏 n(n+1)(n+2)偲弌偟偰偔傞丏
丂乽孨偼丆偙偺栤戣傪尒偨搑抂夝偑傢偐偭偨偹乿偲恞偹傞偲丆乽僴僢丆僴僀乿偲濨枂側昞忣偱丆惗曉帠傪曉偟偰偔傞丏乽偠傖夝傪尒偰壗偵婥晅偔丠乿
丂乽僴僀丆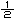 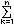 k(k+1) 偺寢壥偲摨偠偱偡乿偲偄偆摎偊偑曉偭偰偔傞丏乽傢偐傞偐乿乽傢偐傝傑偟偨乿乽偠傖愢柧偟偰偛傜傫乿I孨偑崟斅偺慜偵弌偰棃偰丆恾傪昤偄偰愢柧偡傞丏廲k丆墶1丆崅偝 n-k+1 偺捈曽懱乮k=1,2,乧,n乯n 屄傪壛偊偨棫懱偺懱愊偼丆 k(k+1) 偺寢壥偲摨偠偱偡乿偲偄偆摎偊偑曉偭偰偔傞丏乽傢偐傞偐乿乽傢偐傝傑偟偨乿乽偠傖愢柧偟偰偛傜傫乿I孨偑崟斅偺慜偵弌偰棃偰丆恾傪昤偄偰愢柧偡傞丏廲k丆墶1丆崅偝 n-k+1 偺捈曽懱乮k=1,2,乧,n乯n 屄傪壛偊偨棫懱偺懱愊偼丆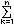 ( (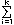 i) 摍偟偄偙偲傪弎傋傞丏乮壓恾嶲徠乯 i) 摍偟偄偙偲傪弎傋傞丏乮壓恾嶲徠乯
丂偦偆偄偊偽崅1偺偲偒丆a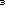 +b +b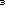 =(a+b)(a =(a+b)(a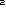 -ab+b -ab+b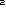 )乮a,b偼惓傑偨偼晧乯偺棫懱儌僨儖傪峫偊偰偔傟偨偺傕I孨偩偭偨丏傗偭偲僋儔僗偺戝敿偑丆偦偆偄偆偙偲偩偭偨偺偐偲偄偆婄傪偟偰偄傞丏 )乮a,b偼惓傑偨偼晧乯偺棫懱儌僨儖傪峫偊偰偔傟偨偺傕I孨偩偭偨丏傗偭偲僋儔僗偺戝敿偑丆偦偆偄偆偙偲偩偭偨偺偐偲偄偆婄傪偟偰偄傞丏
丂乽愭惗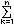 (2k-1)(n-k+1)= (2k-1)(n-k+1)=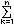 k k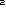 傕偄偊傑偡乿乽偝偡偑揤嵥H偩両乿乽奆傕峫偊偰傒傛偆乿偟偽傜偔奺帺偵峫偊偝偣傞丏 傕偄偊傑偡乿乽偝偡偑揤嵥H偩両乿乽奆傕峫偊偰傒傛偆乿偟偽傜偔奺帺偵峫偊偝偣傞丏
丂摨偠偔H偑恾傪昤偄偰敪昞偡傞丏偟偽傜偔偟偰丆O孨偑丆乽愭惗偺掕媊偝傟偨傛偆側丆棫懱偺懱愊傪媮傔傞偺偵儼婰崋偼堦掕偺曽岦偵壛偊傞偙偲傪嫮惂偟偰偄傑偡偹丏2偮偺椺偺傛偆偵丆偼偠傔偲捈妏偺曽岦偵壛偊偨傝丆偁傞偄偼僕僌僓僌偵壛偊偨傝傕偭偲堦斒壔偱偒傑偣傫偐丠乿乽偆偆傫丆偄偄敪憐偩丆愭惗傕偦偙傑偱偼峫偊偰偄偨偺偩偑丆椺偊偽捈妏曽岦偵壛偊傞偺傪 (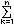 f(k)) f(k))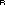 偲昞偡偲丆 ( 偲昞偡偲丆 (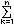 f(k)) f(k))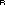 = = 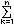 g(k) 偱I孨傗H孨偺傛偆側愢柧側偟偵娙扨偵媮傑傞傕偺偑偐側傝偁傞偹丏悢妛戝岲偒恖娫偺尋媶壽戣偩偹乿慜偺庼嬈偱亀 g(k) 偱I孨傗H孨偺傛偆側愢柧側偟偵娙扨偵媮傑傞傕偺偑偐側傝偁傞偹丏悢妛戝岲偒恖娫偺尋媶壽戣偩偹乿慜偺庼嬈偱亀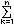 k(k+1)(k+2)乧(k+r)亁偲崟斅偵彂偄偰偄傞偲丆乽僴僀丆乧偱偡乿夽乮偝偒偑偗乯壆偝傫偺T孨偑摎偊傪尵偭偰偔傟傞丏乽偙傟傪棙梡偡傞偲 k(k+1)(k+2)乧(k+r)亁偲崟斅偵彂偄偰偄傞偲丆乽僴僀丆乧偱偡乿夽乮偝偒偑偗乯壆偝傫偺T孨偑摎偊傪尵偭偰偔傟傞丏乽偙傟傪棙梡偡傞偲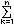 k k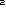 = =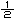 { {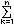 (k-1)k+ (k-1)k+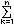 k(k+1)}丆偩偐傜奆傕 k(k+1)}丆偩偐傜奆傕 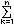 k k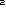 傪媮傔偰偛傜傫乿乽愭惗乿乽愭惗乿T孨丆F孨丆H'孨偑庤傪偁偘傞丏乽慜偵弌偰崟斅偵彂偗乿乽F孨丆H'孨偺夝傪傒傞偲丆傛傝堦斒壔偱偒偦偆偩偹乿 傪媮傔偰偛傜傫乿乽愭惗乿乽愭惗乿T孨丆F孨丆H'孨偑庤傪偁偘傞丏乽慜偵弌偰崟斅偵彂偗乿乽F孨丆H'孨偺夝傪傒傞偲丆傛傝堦斒壔偱偒偦偆偩偹乿
F孨丗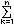 k k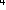 = =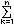 [ [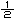 {(k-2)(k-1)k(k+1)+(k-1)k(k+1)(k+2)}+k {(k-2)(k-1)k(k+1)+(k-1)k(k+1)(k+2)}+k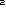 ] ]
丂丂丂丂丂= 乧 =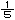 n n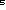 + +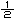 n n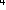 + +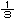 n n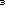 - -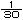 n n
H'孨丗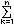 k k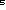 = =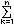 {(k-2)(k-1)k(k+1)(k+2)+5(k-1)k(k+1)+k}= 乧 {(k-2)(k-1)k(k+1)(k+2)+5(k-1)k(k+1)+k}= 乧
丂乽崱擔偺庼嬈偼廩幚偟偰偄偨偹乿乽僴僀丆廔傢傝乿媺挿乽婲棫丆楃乿
2丏sin15亱丆cos15亱丆sin75亱丆cos75亱
丂15亱丆75亱偺嶰妏斾傪媮傔傞抜偵側偭偰丆偼偨偲崲偭偰偟傑偭偨丏O孨偑乽愭惗丆崱傑偱偵廗偭偨抦幆偱偼夝偗傑偣傫乿偲偒偨丏H''孨乽悢嘥傪傗傞慜偵悢A傪傗傞傋偒偩偭偨傫偠傖側偄偱偡偐乿偲偍偭偟傖傞丏乽夝偗側偄偲偼丆夝偄偰偐傜尵偊両偦傟偵屻傠岦偒偺敪憐偼偁偐傫丆愭惗傕崱斀徣偟偰偄傞偲偙傠偩両乿Y孨乽梫偼2廳崻崋偺揥奐傪巊傢側偒傖偄偄偠傖側偄偱偡偐乿乽偦偺捠傝偩丆慜岦偒偺敪憐偩乿乽偊傜偄乿偟偽傜偔恾1傪崟斅偵昤偄偰丆偄傠偄傠曗彆慄傪擖傟偨傝偟偰峫偊偰偄偨丏偦偟偰丆恾2傪敪尒偟偨丏摨帪偵揤嵥H孨傕傢偐偭偨偲惡傪偁偘偨丏巹傕偄偝偝偐嫽暠偟偰偄偨傜偟偄丏偄偮傕偺傛偆偵惗搆偵愢柧偝偣傞偺傪朰傟偰偟傑偭偨丏乽愭惗偡偽傜偟偄夝偱偡偹乿乽偦偆偩側乿傑傫偞傜偱傕側偄婄傪偟偰偄傞偲丆乽愭惗丆壗枩墌偖傜偄偺壙抣偑偁傝傑偡偐乿偲偨偨傒妡偗偰偒偨丏Y孨偵偼偪傚偭偲娞傪敳偐傟偨偑丆偦偙偼儀僥儔儞嫵巘偺娧榎偱丆乽傑偁埨偔尒愊傕偭偰100枩偖傜偄偐側乿堦弖僋儔僗偺慡堳偐傜偺懜宧偺娽嵎偟丏乽偙偺Idea丆cos36亱丆sin36亱偵傕巊偊側偄偐側丏偄偄夝偵偼徿嬥傪弌偦偆乿
丂斵傜偼懖嬈偟偰偟傑偭偨丏枹夝寛偺傑傑偱偁傞丏
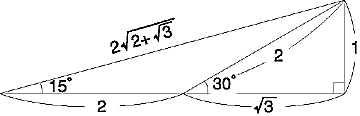
恾1
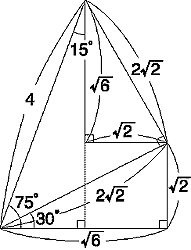
恾2
sin75亱=cos15亱=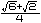
sin15亱=cos75亱=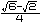
3丏 媴偺懱愊
丂乽媴偺懱愊偼偳偆偟偰媮傔傞偐乿乽尨揰拞怱偺敿墌偺夞揮懱偺懱愊乿偲摎偊傞偺偑偄傞丏乽孨偼愊暘傪妛傇傑偱媴偺懱愊偺媮傔曽偵偮偄偰峫偊偨偙偲偼側偄偺丠乿乽拞妛惗偱傕慡堳棟夝偱偒傞曽朄偩乿偲尵偆偲媫偵懱傪忔傝弌偟偰偒偨丏斵傜偼嶼悢偼摼堄拞偺摼堄偩丏乽媮傔曽偼抦傜傫偱傕丆掙柺偺敿宎r丆崅偝2r偺墌拰丆摨偠敿宎偱丆崅偝偑敿暘偺墌悕2偮偺懱愊偖傜偄媮傑傞偩傠偆乿崱擔偺庼嬈偼傗傗挧敪揑偵恑傔傞偙偲偲偡傞丏乽偦傟偑偳偆偐偟偨傫偱偡偐乿椺偵傛偭偰Y孨偩丏乽偦傟偼偙偭偪偺暦偒偨偄偙偲偩乿崟斅偵媴偲墌拰傪昤偔丏N孨偑庤傪偁偘偰乽僴僀丆媴偺懱愊偵墌悕2偮偺懱愊傪壛偊傞偲墌拰偺懱愊偵側傝傑偡乿乽偮傑傝媴偺懱愊偼墌拰偺懱愊偐傜2偮偺墌悕偺懱愊傪傂偄偨傕偺偵摍偟偄傢偗偩側乿僯儎儕偲徫偭偰傢偞偲溴滂(偙傫偵傖偔)栤摎傪偟偰偍偔丏斵偺僲乕僩偵偼恾3偑昤偄偰偁傞丏乽偪傚偭偲戄偟偰偹乿偲斵偺僲乕僩傪奆偵怳傝偐偞偟偰尒偣傞丏斅彂偡傞丏
丂乽愭惗丆媴偼愒摴嬤偔偑懱愊偑戝偒偔偰丆椉嬌偼尷傝側偔0偵嬤偄偺偵丆墌拰偺巆傝偺晹暘偺懱愊偼丆斵偺恾偼媡偠傖側偄偱偡偐乿偲K孨丏乽孨偺敪尵偺慜敿偼堄枴晄徻丆慡慠晄惓妋偩偑杮幙傪偮偄偰偼偄傞乿乽愭惗偺尵偭偰偄傞偙偲偼丆帺屓柕弬偩乿偲傗偠傞搝偑偄傞丏乽偄偄敪憐偩丆偠傖偁丆偙偆偟偰傒傛偆乿墌拰偺拞偵2偮偺墌悕傪彂偒崬傫偱偄偔丏乮恾4乯
丂W孨偺僲乕僩偼丆恾4偵媴傕撪愙偝偣偰偄傞丏斵偺僲乕僩傪巜偝偟偰乽偙偺Idea傪傕傜偭偨傢偗偩乿媴偲墌拰偲2偮偺墌悕偺堦曽偵抐柺傪怓僠儑乕僋偱彂偒崬傓丏乽僇償傽儕僄儕偺掕棟傪抦偭偰偄傞偩傠偆丏偦偄偮傪奼挘偟偨傛偆側傕偺偩乿乽僴僀乿F孨偑庤傪忋偘傞丏乽愢柧偼孨偵傑偐偣傞丏乧乿
丂兾=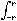 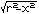 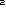 dx=兾 dx=兾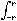 r r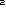 dx-兾 dx-兾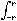 x x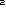 dx dx
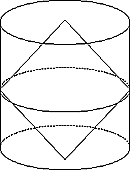
恾3
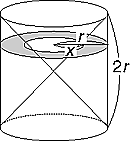
恾4
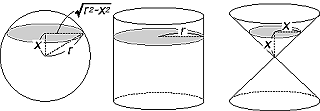
4丏 媴偺昞柺愊
丂乽媴偺昞柺愊偼丠乿乽4兾r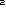 偱偡乿寉曁偟偨傛偆側娽嵎偟丏乽掙柺偑敿宎r偺墌偱崅偝2r偺墌拰偺懁柺愊偼丠乿傾僢偲偄偆姶偠偱丆媫偵暤埻婥偑恀柺栚偵側傞丏乽愭惗丆媴偺昞柺愊偼墌拰偺懁柺愊偵摍偟偄傫偱偡偐乿椺偺夽壆偝傫偱偁傞丏乽傑偨扙慄偱偡偐乿拑乆偑擖傞丏乽乬Mathematics is derailments itself.乭偩両乿乽姤帉偼丠乿乽娭怱偼側偄乿乽傑偢偆乿乽敿媴偲敿媴偵奜愙偡傞墌悕偺岎傢傝偺墌偺忋丆壓曣慄偵偦偭偰 偱偡乿寉曁偟偨傛偆側娽嵎偟丏乽掙柺偑敿宎r偺墌偱崅偝2r偺墌拰偺懁柺愊偼丠乿傾僢偲偄偆姶偠偱丆媫偵暤埻婥偑恀柺栚偵側傞丏乽愭惗丆媴偺昞柺愊偼墌拰偺懁柺愊偵摍偟偄傫偱偡偐乿椺偺夽壆偝傫偱偁傞丏乽傑偨扙慄偱偡偐乿拑乆偑擖傞丏乽乬Mathematics is derailments itself.乭偩両乿乽姤帉偼丠乿乽娭怱偼側偄乿乽傑偢偆乿乽敿媴偲敿媴偵奜愙偡傞墌悕偺岎傢傝偺墌偺忋丆壓曣慄偵偦偭偰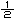 偢偮偺偲偙傠偱丆墌悕傪愗傞偲墌悕戜偑偱偒傞傗傠乿乽敿媴偺敿宎r丆墌悕偺拞怱慄偲曣慄偺側偡妏傪兤偲偡傞偲丆偝偒偺墌悕戜偺懁柺愊偼2兾r cos兤傗乿乽偳偆偟偰偱偡偐丏Pappus Guldin偺掕棟傪巊偆傫偱偡偐乿乽偳偭偪偱傕偊偊丆敿宎r丆曣慄偺挿偝l偺墌悕偺懁柺愊S偼丠乿乽僴僀丆S=兾rl偱偡乿乽帺暘偱摫偗傞傗傠乿乽崱擔偺彲愭惗捒偟偔掅婥埑傗側偁乿乽偝偭偒偺岎傢傝偺墌偺拞怱偵捈慄忬偺岝尮傪偍偄偰丆偙偺敿媴偵奜愙偡傞墌拰偺僗僋儕乕儞偵丆墌悕戜偺懁柺傪幨偟弌偟偰傒偄丏僥乕僾偱嶌偭偨椫偺傛偆側憸偑偱偒傞傗傠乿乽乧乿乽懁柺愊偼丠乿乽岎傢傝偺墌偺敿宎偼 r cos兤 偩偐傜敿宎偼 偢偮偺偲偙傠偱丆墌悕傪愗傞偲墌悕戜偑偱偒傞傗傠乿乽敿媴偺敿宎r丆墌悕偺拞怱慄偲曣慄偺側偡妏傪兤偲偡傞偲丆偝偒偺墌悕戜偺懁柺愊偼2兾r cos兤傗乿乽偳偆偟偰偱偡偐丏Pappus Guldin偺掕棟傪巊偆傫偱偡偐乿乽偳偭偪偱傕偊偊丆敿宎r丆曣慄偺挿偝l偺墌悕偺懁柺愊S偼丠乿乽僴僀丆S=兾rl偱偡乿乽帺暘偱摫偗傞傗傠乿乽崱擔偺彲愭惗捒偟偔掅婥埑傗側偁乿乽偝偭偒偺岎傢傝偺墌偺拞怱偵捈慄忬偺岝尮傪偍偄偰丆偙偺敿媴偵奜愙偡傞墌拰偺僗僋儕乕儞偵丆墌悕戜偺懁柺傪幨偟弌偟偰傒偄丏僥乕僾偱嶌偭偨椫偺傛偆側憸偑偱偒傞傗傠乿乽乧乿乽懁柺愊偼丠乿乽岎傢傝偺墌偺敿宎偼 r cos兤 偩偐傜敿宎偼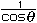 攞丆墌悕戜偺崅偝偼cos兤丏偟偨偑偭偰僥乕僾偺暆傕?乿乽傢偐偭偨乿乽2兾r cos兤亊 攞丆墌悕戜偺崅偝偼cos兤丏偟偨偑偭偰僥乕僾偺暆傕?乿乽傢偐偭偨乿乽2兾r cos兤亊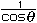 =2兾r乿乽愭掱偼墌悕戜偺曣慄偺挿偝傪l偲偟偨偗傟偳丆兤偼0偐傜 =2兾r乿乽愭掱偼墌悕戜偺曣慄偺挿偝傪l偲偟偨偗傟偳丆兤偼0偐傜 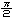 傑偱摦偔偐傜偦偺偆偪偺揔摉側偄偔偮偐偺兤偵懳偟偰奜愙偡傞墌悕戜傪偮偔傝丆偦偺偲偒椬傝崌偆忋壓偺墌悕戜偺壓掙偲忋掙傪嫟桳偡傞傛偆偵偣側偁偐傫偗偳丆壛偊偰偄偔偲傝傫偛偺旂傪僫僀僼偱偖傞偖傞傓偄偨傛偆側棫懱偑偱偒傞傗傠丏墌悕戜偺崅偝偺崌寁偼r偩偐傜丆偙偺棫懱偺懁柺愊偼2兾r亊r=2兾r 傑偱摦偔偐傜偦偺偆偪偺揔摉側偄偔偮偐偺兤偵懳偟偰奜愙偡傞墌悕戜傪偮偔傝丆偦偺偲偒椬傝崌偆忋壓偺墌悕戜偺壓掙偲忋掙傪嫟桳偡傞傛偆偵偣側偁偐傫偗偳丆壛偊偰偄偔偲傝傫偛偺旂傪僫僀僼偱偖傞偖傞傓偄偨傛偆側棫懱偑偱偒傞傗傠丏墌悕戜偺崅偝偺崌寁偼r偩偐傜丆偙偺棫懱偺懁柺愊偼2兾r亊r=2兾r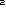 傗乿僴僴儞傢偐偭偨偲偄偆傛偆側婄傪偟偰偄傞偺偑悢柤丆傢偐偭偨傛偆側丆傢偐傜傫傛偆側偺偑悢柤丏偁偲偼慡偔妎偮偐側偄両両乽偦傟偱傗側偁乿乽傓偔傝傫偛偺旂嬓傪偳傫偳傫嵶偔偟偰偄偔偲丆嬌尷偼敿媴偺昞柺愊偩乿偍傟偼傢偐傞偧偲偣偭偣偲僲乕僩偟偰偄傞M孨丆戝懡悢偼偦傟偱傕傢偐傠偆偲昁巰偱搘椡偟偰偄傞丏恾傪昤偔丏 傗乿僴僴儞傢偐偭偨偲偄偆傛偆側婄傪偟偰偄傞偺偑悢柤丆傢偐偭偨傛偆側丆傢偐傜傫傛偆側偺偑悢柤丏偁偲偼慡偔妎偮偐側偄両両乽偦傟偱傗側偁乿乽傓偔傝傫偛偺旂嬓傪偳傫偳傫嵶偔偟偰偄偔偲丆嬌尷偼敿媴偺昞柺愊偩乿偍傟偼傢偐傞偧偲偣偭偣偲僲乕僩偟偰偄傞M孨丆戝懡悢偼偦傟偱傕傢偐傠偆偲昁巰偱搘椡偟偰偄傞丏恾傪昤偔丏
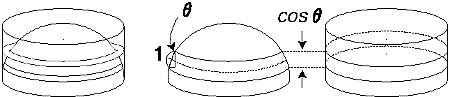
丂偲偙傠偱桳傝擄偄偙偲偵丆旂嬓偼懢偔偰傕嵶偔偰傕墌悕戜偺崅偝偺榓偑r偱偁傝偝偊偡傟偽昞柺愊偼墌拰偺懁柺愊2兾r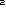 偵摍偟偄傫偩偐傜丆敿媴偺昞柺愊偼2兾r 偵摍偟偄傫偩偐傜丆敿媴偺昞柺愊偼2兾r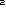 偩丏嬌抂側応崌偼兤= 偩丏嬌抂側応崌偼兤=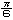 偺偲偒偺墌悕壓敿暘偺懁柺愊偵摍偟偄丏偙傟偼墌悕偺懁柺愊偺 偺偲偒偺墌悕壓敿暘偺懁柺愊偵摍偟偄丏偙傟偼墌悕偺懁柺愊偺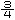 偩偐傜憡帡斾 偩偐傜憡帡斾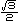 偱弅彫偟偨墌悕丗敿媴偲掙柺傪嫟桳偟丆掙柺偲曣慄偺側偡妏偑60亱偺墌悕偺懁柺愊偵丆偟偨偑偭偰丆掙柺偺墌2枃偺柺愊偵傕摍偟偄丏 偱弅彫偟偨墌悕丗敿媴偲掙柺傪嫟桳偟丆掙柺偲曣慄偺側偡妏偑60亱偺墌悕偺懁柺愊偵丆偟偨偑偭偰丆掙柺偺墌2枃偺柺愊偵傕摍偟偄丏
丂乽偁偭丆偝偭偒偺偼S=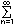 Sn= Sn=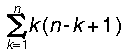 2兾r 2兾r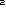 =2兾r =2兾r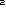 偩丏偦傟偵媴偼敿媴偺攞偩乿乽偁偨傝慜偺偙偲偩乿乽崱擔偺庼嬈偼偪傚偭偲峳傟偰偄傑偟偨偹乿乽愭惗丆壗偑尵偄偨偄傫偱偡偐乿乽崱擔偺庼嬈偼嵟埆偠傖丆晛抜偳傫側偵傛偔傢偐傞庼嬈傪偟偰偄偨偐傛偔傢偐偭偨傠偆乿慡堳柇偵擺摼乧丠両乽偦傟偱偼廔傢傝乿乽婲棫丆楃乿怱抧傛偄旀傟偑巆偭偨丏 偩丏偦傟偵媴偼敿媴偺攞偩乿乽偁偨傝慜偺偙偲偩乿乽崱擔偺庼嬈偼偪傚偭偲峳傟偰偄傑偟偨偹乿乽愭惗丆壗偑尵偄偨偄傫偱偡偐乿乽崱擔偺庼嬈偼嵟埆偠傖丆晛抜偳傫側偵傛偔傢偐傞庼嬈傪偟偰偄偨偐傛偔傢偐偭偨傠偆乿慡堳柇偵擺摼乧丠両乽偦傟偱偼廔傢傝乿乽婲棫丆楃乿怱抧傛偄旀傟偑巆偭偨丏 |
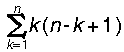
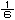 n(n+1)(n+2)偲弌偟偰偔傞丏
n(n+1)(n+2)偲弌偟偰偔傞丏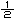
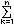 k(k+1) 偺寢壥偲摨偠偱偡乿偲偄偆摎偊偑曉偭偰偔傞丏乽傢偐傞偐乿乽傢偐傝傑偟偨乿乽偠傖愢柧偟偰偛傜傫乿I孨偑崟斅偺慜偵弌偰棃偰丆恾傪昤偄偰愢柧偡傞丏廲k丆墶1丆崅偝 n-k+1 偺捈曽懱乮k=1,2,乧,n乯n 屄傪壛偊偨棫懱偺懱愊偼丆
k(k+1) 偺寢壥偲摨偠偱偡乿偲偄偆摎偊偑曉偭偰偔傞丏乽傢偐傞偐乿乽傢偐傝傑偟偨乿乽偠傖愢柧偟偰偛傜傫乿I孨偑崟斅偺慜偵弌偰棃偰丆恾傪昤偄偰愢柧偡傞丏廲k丆墶1丆崅偝 n-k+1 偺捈曽懱乮k=1,2,乧,n乯n 屄傪壛偊偨棫懱偺懱愊偼丆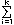 i) 摍偟偄偙偲傪弎傋傞丏乮壓恾嶲徠乯
i) 摍偟偄偙偲傪弎傋傞丏乮壓恾嶲徠乯
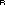 偲昞偡偲丆 (
偲昞偡偲丆 (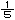 n
n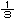 n
n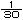 n
n

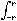
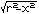



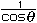 攞丆墌悕戜偺崅偝偼cos兤丏偟偨偑偭偰僥乕僾偺暆傕?乿乽傢偐偭偨乿乽2兾r cos兤亊
攞丆墌悕戜偺崅偝偼cos兤丏偟偨偑偭偰僥乕僾偺暆傕?乿乽傢偐偭偨乿乽2兾r cos兤亊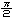 傑偱摦偔偐傜偦偺偆偪偺揔摉側偄偔偮偐偺兤偵懳偟偰奜愙偡傞墌悕戜傪偮偔傝丆偦偺偲偒椬傝崌偆忋壓偺墌悕戜偺壓掙偲忋掙傪嫟桳偡傞傛偆偵偣側偁偐傫偗偳丆壛偊偰偄偔偲傝傫偛偺旂傪僫僀僼偱偖傞偖傞傓偄偨傛偆側棫懱偑偱偒傞傗傠丏墌悕戜偺崅偝偺崌寁偼r偩偐傜丆偙偺棫懱偺懁柺愊偼2兾r亊r=2兾r
傑偱摦偔偐傜偦偺偆偪偺揔摉側偄偔偮偐偺兤偵懳偟偰奜愙偡傞墌悕戜傪偮偔傝丆偦偺偲偒椬傝崌偆忋壓偺墌悕戜偺壓掙偲忋掙傪嫟桳偡傞傛偆偵偣側偁偐傫偗偳丆壛偊偰偄偔偲傝傫偛偺旂傪僫僀僼偱偖傞偖傞傓偄偨傛偆側棫懱偑偱偒傞傗傠丏墌悕戜偺崅偝偺崌寁偼r偩偐傜丆偙偺棫懱偺懁柺愊偼2兾r亊r=2兾r
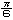 偺偲偒偺墌悕壓敿暘偺懁柺愊偵摍偟偄丏偙傟偼墌悕偺懁柺愊偺
偺偲偒偺墌悕壓敿暘偺懁柺愊偵摍偟偄丏偙傟偼墌悕偺懁柺愊偺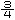 偩偐傜憡帡斾
偩偐傜憡帡斾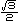 偱弅彫偟偨墌悕丗敿媴偲掙柺傪嫟桳偟丆掙柺偲曣慄偺側偡妏偑60亱偺墌悕偺懁柺愊偵丆偟偨偑偭偰丆掙柺偺墌2枃偺柺愊偵傕摍偟偄丏
偱弅彫偟偨墌悕丗敿媴偲掙柺傪嫟桳偟丆掙柺偲曣慄偺側偡妏偑60亱偺墌悕偺懁柺愊偵丆偟偨偑偭偰丆掙柺偺墌2枃偺柺愊偵傕摍偟偄丏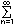 Sn=
Sn=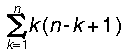 2兾r
2兾r