| 授業実践記録 | |
| 場合の数・確率の単元で魅力ある授業をめざして | |
| 兵庫県立北摂三田高等学校 山崎俊喜 |
|
|
1.はじめに
|
|
| 今年度、兵庫県立北摂三田高等学校に異動した。本校は、県下でも有数の進学校である。今年度の進学実績では、国公立大学169名である。 全体の特徴として、非常に勉強熱心である。授業以外の行事についても自分たちで中心となって取り組んでいる。何事においても生徒は前向きである。 今年度1年生の授業を担当している。苦手意識はあるものの、本当に理解していない生徒はほとんどいない。しかしながら、数学の単元によっては、苦手としている生徒は少なくない。 |
|
|
2.場合の数・確率について
|
|
| 場合の数・確率という単元について、本校に限らず、苦手としている生徒が多い。私自身も教師になるまでは、場合の数・確率については、苦手意識を持っていた。 どうして苦手意識を持つかというと、次の2点が考えられる。
[1] については、国語と関連してくる。読解力がないと問題の意味を理解することはできない。私自身も国語が苦手であったため、苦労することが多かった。 |
|
|
3.場合の数・確率の指導方法について
|
|
どの公式を使えばよいかについては、キーワードが出てくるので、そこを強調するようにしている。順列については、「並べる」。組合せについては「選ぶだけ。並べない」ということを強調している。 コインやサイコロを投げる場合などは、「反復試行」を意識させるようにしている(必ずしも、反復試行として考えなくてもよい場合もある。)
例1は順列、例2、3は組合せの問題である。例1では、「選ぶ」という言葉があるが、部長、副部長、マネージャーという順に並べているということを確認する必要がある。例2、3では、「取り出す」に注意し、「選ぶ」だけであるということを確認する必要がある。一度、順列・組合せの内容で、小テストをすると、どちらの公式を使うのかがはっきりする(反復試行については、別途取り上げる方が効果的である。)
一瞬難しく感じるかもしれないが、本校生に問題を解かせたところ、難しく感じることなく、すぐに解答を導けた。
この内容については、「同じ種類の10個のお菓子を3人で自由に分ける方法は何通りあるか。ただし、1人に1個は必ず与えること。」と同じであることを示した上で、あなたが、親で3人の子どもに分けさせるにはどうすればよいかを考えさせた。そうすると、まず1人1個ずつ与えて、残り7個を3人で分ければよい。つまり、○7個と|(仕切り)2本の並び替え ○○○○○○○|| の順列ということで、図をかき、 |
|
|
4.おわりに
|
|
| 今後とも、ヒントを与えながら、身近な問題に置き換え、イメージを大切にした授業を続けていきたいと考えている。 |
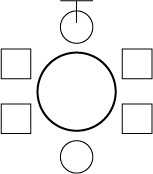 (考え方)□は男子、○は女子を表している。円順列は回転して同じ並び方になるものは同じと考えるので、1人を固定し、回転しないようにする必要がある。そのため、誰かを固定する必要があるが、誰を固定するのかが、解答のポイントになる。固定したことを表す記号として、
(考え方)□は男子、○は女子を表している。円順列は回転して同じ並び方になるものは同じと考えるので、1人を固定し、回転しないようにする必要がある。そのため、誰かを固定する必要があるが、誰を固定するのかが、解答のポイントになる。固定したことを表す記号として、