E = 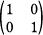 , I = , I = 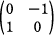 , O = , O = 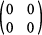 とおく。 とおく。
このとき,複素数 z =x + yi と行列 Z = 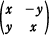 = xE +yI とは1対1に対応する。 = xE +yI とは1対1に対応する。
さらに,加減乗除についても対応していることがわかる。
実際,複素数 α = x + yi , β = s + ti にそれぞれ行列 A =xE +yI, B =sE +tI を対応させるとき,
| α+β = (x +s )+(y +t )i |
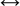 |
(x +s ) E +(y +t ) I = A+B |
| α−β= (x −s)+(y −t )i |
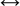 |
(x −s) E +(y −t ) I = A−B |
| αβ =(xs −yt )+(xt +ys )i |
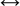 |
(xs −yt ) E +(xt +ys ) I = AB (=BA ) |
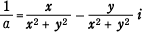 |
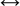 |
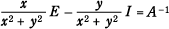 |
となる。また,x = y =0 すなわち A =O の場合以外は,A は逆行列をもつ。
M = {xE +yI | x, y は実数 } とするとき,M は「複素数を表す行列」全体の集合であり,このような行列だけを考えたとき,四則演算に関して複素数全体の集合Cと同じ「構造」を持つのである。
複素数を表す行列は,互いに交換可能であることにも注意したい。
これは大学入試問題でも頻出である。次の広島大の問題を見てみよう。
|
例題1.
複素数 x + yi に行列 X = 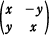 を対応させ,この行列 X を複素数 x + yi に対応する行列という。ここに,x, y は実数で,i は虚数単位を表す。 を対応させ,この行列 X を複素数 x + yi に対応する行列という。ここに,x, y は実数で,i は虚数単位を表す。
| (1) |
1および i に対応する行列をそれぞれ求めよ。
|
| (2) |
複素数 a +bi に対応する行列を A, 複素数 c +di に対応する行列を B とするとき,複素数の積 (a +bi ) (c +di ) に対応する行列は AB であることを示せ。 |
[1997年度 広島大]
|
(1)について,1に単位行列 E が対応し,虚数単位 i には 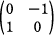 が対応する。 が対応する。
(2)については,複素数を表す行列が,積について対応していることを示す問題である。
次は,和の対応および方程式の対応を示す問題である。
|
例題2.
E = 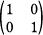 , I = , I = 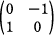 , O = , O = 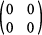 とおく。M = {xE +yI | x, y は実数 } とするとき, とおく。M = {xE +yI | x, y は実数 } とするとき,
| (1) |
A =xE +yI , B =sE +tI とおいて,A , B∈M ならば A +B∈M, A−B∈M を示せ。
|
| (2) |
A , B∈M ならば AB = BA∈M を示せ。
|
| (3) |
A∈M, A≠O ならば A の逆行列 A−1 が存在し,A−1∈M となることを示せ。
|
| (4) |
Z ∈M, Z 4 = E を満たす Z をすべて求めよ。
|
| (5) |
Z 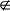 M, Z 4 = E を満たす2×2行列 Z はあるか。あれば例を1つ挙げよ。なければそのことを証明せよ。 M, Z 4 = E を満たす2×2行列 Z はあるか。あれば例を1つ挙げよ。なければそのことを証明せよ。 |
[2006年度 大阪医大]
|
例題2の (1), (2), (3) で,加法,乗法と逆数の対応を導いている。
特に,(2) では複素数を表す行列が,互いに交換可能であることを述べている。
(4) の方程式 Z 4 = E は,複素数の方程式 z 4= 1 に対応する。
z 4= 1 の解は z =±1, ±i であるから,これに対応する行列 Z =±E, ±I が解となる。
ただし4次方程式に帰着できるのは,Z∈M の条件があるからである。この条件を失えば
Z =±E, ±I 以外にも Z 4 = E を満たす行列が存在する。例えば Z= 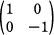 である。 である。
これが (5) の出題意図である。
次も方程式の対応である。
A は複素数を表す行列である。A に対応する複素数を z とする。
(1)の A2= J は z 2 = i を意味する。z =± 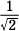 (1+i ) だから,A =± (1+i ) だから,A =±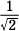 (E +J ) である。 (E +J ) である。
(2)は,複素数を表す行列の集合 M = {xE +yJ | x, y は実数 } の要素 A, B に対して,
AB = O ならば A = O または B = O
が成り立つことを示す問題である。すなわち,Mには零因子が存在しないのである。
証明は簡単である。AB = O において両辺の行列式をとると,
det (AB ) = det (O )
行列式の性質を用いて
det (A ) det (B ) = 0
であるから,( a12+b12 ) ( a22+b22 ) = 0 となる。これより,題意が示せる。
A≠O ならば,M の要素 A は必ず逆行列を持つことがわかる。
|
例題4.
行列 I と J が I = 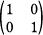 , J = , J = 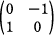 であるとき, であるとき,
| (1) |
行列 J 2, J 3, J 4 は,それぞれ I または J の定数倍になることを示せ。
|
| (2) |
実数 a と b について,行列 aI +bJ が逆行列を持つための必要十分条件を求めよ。
|
| (3) |
任意の実数 s, t に対して,行列 sI +(1+st ) J +tJ 2+st 2J 3+t 2J 4 は逆行列をもつことを示せ。 |
[2005年度 広島大]
|
この例題では,I が1に,J が虚数単位 i に対応している。
(1) では,i 2 =−1 , i 3 =−i , i 4 = 1 に対応して,J 2=−I, J 3 =−J , J 4 = I が成り立つことが分かる。
また,(2) では,a +bi が逆数をもつ条件と同等であることに注意したい。先程と同様,a = b =0 のとき以外は,aI +bJ は逆行列を持つのである。
(3) は,
sI +(1+st ) J +tJ 2+st 2 J 3+t 2 J 4 =(s−t +t 2) I + (1+st−st 2) J
となるから,複素数 (s−t +t 2)+(1+st−st 2) i が逆数をもつかどうかに帰着される
|