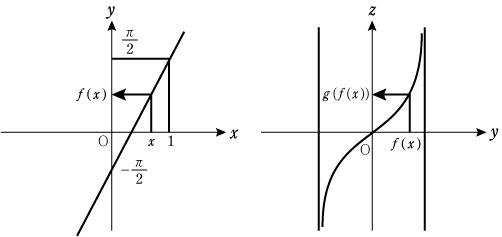授業実践記録
『連続体濃度 』を教えよう
武蔵工業大学付属高等学校
田口哲夫
　
1．はじめに
　中学生に対しては，ユークリッド原論の公理，公準を提示し，『幾何』を，公理主義的に唱え，第5の公準の重要性を強調し平行線の同位角や錯角の定理（性質）に結びつけている。また，『代数』においても，『相等しいものから相等しいものを加えても引いても相等しい』等の公理からの導入をすることで，絶対的な真理として『三角形の内角の和は180度』『三平方の定理』等が，生徒達の脳裏に焼き付く結果になっている。その後，生徒達にとっては，量（面積や角度や長さ）として出現していた数が，比で表せない無理量となり，ピタゴラス学派によってなされた背理法による証明から無理数が存在すると決定付けさせる。この無理数を利用して，アルファーリズミーの手法を使って，2次方程式を面積に帰着させ平方完成させて解いて見せる。これを一般化し，2次方程式の解の公式を導く。さらにカルダノの手法をつかって，3次方程式を体積に帰着させて自分で，解いてみることによって，生徒達にも，カルダノのパラドックスが起こり虚数（ i ）を鮮明に定義させることとなる。
　総合学習や数学クラブ等の場面では，生徒は独自に研究に入る。数学史の数の拡張を知り，自然数は単に物を数える道具としての存在するものではないことを知る。すなわち，ペアノの公理によって自然数を公理的に再定義し，その後，拡張され，整数を2項関係化することでグラフが表れる。クロネッカーによって有理数（a, b）（a, b∈Z ）表記が行われ再体系化されることを知る。その後，大学において，『デデキントの切断公理から実数の連続性，コーシーの収束条件』の一連の流れを学び，数の拡張として『四元数』へとつながっていきベクトル空間や次元等の研究から数学者の志しを我がものにすることになる。
　さて，ガリレオ・ガリレイが，自然数が平方数と1対1に対応することを示し，無限集合ではユークリッド原論の『全体は部分より大きい』という公理が成り立たないと指摘した。それに継いで『全部の集合を集めた集合はもはや集合ではない』とラッセルのパラドックスが起こる。さらに学生達は，ヒルベルトの公理・形式主義による『幾何学基礎論』によって神秘性・論理性が強まり，ますます学問への興味関心意欲が湧いてくる。
　さて，中学高校教科書の中から，『写像の定義』すなわち関数の厳密な定義が消え，数学という学問の本質への誘い，現代数学の基本の入り口ともいうべき内容がなくなって久しい。写像の定義・定理が，概念形成されなければ，大学入学後の学力の低下（リメデイアル教育）や他分野の学問への理解能力に大きく影響する。特に，大学入試問題においては，解くときの厳密性や，いま解いている問題が『数学の問題』なのか『無味乾燥な計算問題』なのか識別ができなくなり，解いたことにはならない。『解き導くこと』は『証明すること』と同様に，数学にて定義する『関係』そのものを利用して導く論理力のいる同等作業なのである。
　純粋数学だけではなく，産業界，経済界，とりわけ昨今では電子署名，金融市場の取引，コンビナートなどの工学設計といった応用数学への理解が叫ばれている中で，PISA型の学習指導要領に改定される今だからこそ，今一度，高校生や大学生に対して，数学の最も基礎基本であり，大学の数学を理解するために必要な，写像の入門を説明したい。本文は，写像の定義から神秘的なカントールによって導入された『集合の濃度』の理解を促し，高校生や大学生に対して，数学の論理性・厳密性を再認識させる試みである。
　
2．写像の定義と同値関係
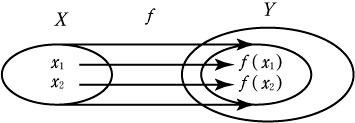
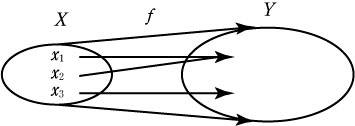
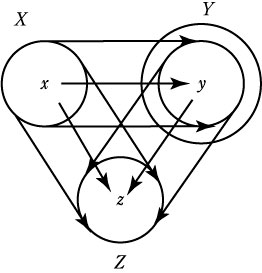
　厳密に写像の定義を理解させよう。ただし，関数は写像の一種であることを生徒達に理解させる。
　定義　集合 X のすべての要素から，集合Y の要素をただ一つ対応させるとき，対応 f を集合X から集合Y への写像であるという。
　　　f : X →Y
　次に，写像について四つの非常に重要な性質を考えて分類していく。

定義1（単射：1対1の写像）
　f : X →Y が単射であるとは，x1, x2∈X について，
　　　x1≠x2 ならば，f (x1)≠f (x2) が成り立つことである。
　　　すなわち，∀x1，x2 ∈A，x1≠x2 ⇒ f (x1)≠f (x2)
イメージ図は重要だ。


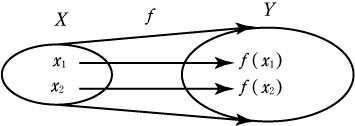
定義2（全射：上への写像）
　f : X →Y が全射であるとは，Y の任意の要素 y に対して
　　　　y = f (x)
となる X の要素 x が少なくとも一つ存在することである。
　　　すなわち，∀y∈Y，∃x∈X，Y = f (x)


定義3（全単射:上への1対1の写像）
　f : X →Y が全単射であるとは，Y の任意の要素 y に対して
　　　　y = f (x)
となるX の要素 x がただ一つ存在することである。
　　　このとき，x = f -1(y)（逆写像）が存在する。


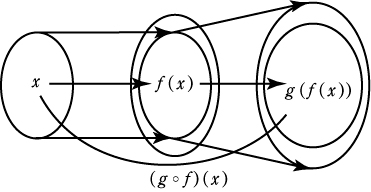
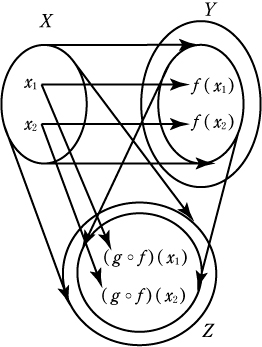
定義4（合成写像）
　2つの写像 f : X →Y ，g : Y →Z について，要素 x∈X に対し，Z の要素 g (f (x)) を対応させると，集合 X から集合 Z への写像となる。これを f と g の合成写像といい，
gf で表す。
　　　　　　　(gf )(x)=g (f (x))
この式の変形は特に重要である。


　以下の2つの定理を理解しておこう。証明には合成関数の定義を効果的に利用する。

定理1
　f : X →Y ，g : Y →Z において
（1）f，g が共に単射ならば，gf も単射である。

証明　x1，x2 ∈A に対して単射の定義の対偶を利用して
　　 　　(gf )(x1) = (gf )(x2)
　　定義4の合成関数の定義から
　　 　g (f (x1)) = g (f (x2))
　　g は単射であるから
　 　　f (x1) = f (x2)
　　f も単射であるから
　 　　x1= x2　　　(Q. E. D. )

（2）f，g が共に全射ならば，gf も全射である。
　　任意の z ∈Z をとると，まず g が全射より
　　　y ∈Y ，z = g (y )
　　がなりたつ。
　　　さらに，y に対して，f も全射であるから
　　　x ∈X ，y = f (x )
　　となる。よって
　　　z = g (f (x )) = (gf )(x )
となる。　　　(Q. E. D. )

　この（1）（2）は当たりまえに感じるが，数学では厳密に証明する。
　次の定理は証明は若干難しい。イメージ図を書いて十分時間をかけて理解しよう。

定理2
（1）gf が全射ならば，g は全射である。

証明　gf が全射だから
　　任意のz ∈Z をとると
　　　　(gf )(x) = z
　　となる x ∈X に存在する。
　　定義4の合成関数の定義から
　　　g (f (x )) = z となり，
　　z ∈Z に対して，f (x )∈Y が
　　　存在する。g は全射である。

(Q. E. D. )
（2）gf が単射ならば，f は単射である。
証明　gf は単射であるから，対偶を利用して
　　　(gf )(x1) = (gf )(x2)
　　ならば，x1 = x2 がなりたつ。（＊）
　　ここで背理法を利用して
　　 f が単射でないと仮定すると
　　　x1 ≠ x2 ⇒f (x1) =f (x2)
　　　　　　　　 ⇒g (f (x1)) = g (f (x2))
　　定義4の合成関数の定義から
　　　(gf )(x1) = (gf )(x2)
（＊）より，x1 = x2 がなりたつ。
よって，x1 ≠ x2 に矛盾する。f は単射である。

　(Q. E. D. )

定理2の（1），（2）より，
　f : X →Y ，g : Y →X の合成写像 gf も f g も全単射とすると，f も g も全単射となる。このとき，はじめて，f の逆関数が存在して f -1= g であるという。

　ここで，集合 X から集合 Y への全単射（上への1対1対応）があるとき，『対等』であるといい X〜Y と書く。この対等という関係は，次の（1），（2），（3）が成り立つとき『同値関係』があるという。
（1）X 〜X　　　　　　　　（反射律）
（2）X 〜Y ⇒ Y 〜X　　　 　（対称律）
（3）X 〜Y，Y 〜Z ⇒X 〜Z　（推移律）
　
3．集合の濃度
　集合 A が，A 〜{1，2，3，………，n } のとき有限集合という。
　また，有限でない集合を無限集合という。その要素の個数を基数と呼び，Card(A) で表し，Card(A) = n となる。（Card. は Cardinal Number の略）
　そこで，無限集合にも，基数を定義する。
　カント−ルが，自然数 N の濃度の基数に 0 という記号を与えた。
　0 をアレフゼロと読み， はヘブライ文字の第1アルファベットである。
　自然数 N と同じ濃度をもつ集合の濃度を Card(N ) = 0 と書く。
　有限集合で考えていたものを無限集合まで拡大しようという動きである。　

［可付番濃度の定義］
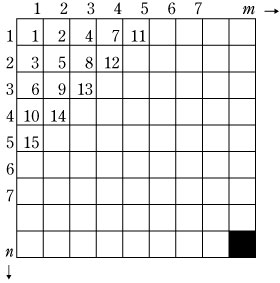
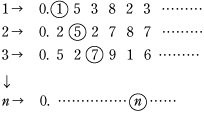
　集合X が可付番集合であるとは，自然数N とX が全単射であることである。この全単射を用いて，X の要素に1対1に自然数の番号を付けることができる集合である。この集合の濃度を下付番集合といい0 で表す。

定理1　整数 Z の集合の濃度は，0 である。
　　0,1,-1,2,-2,3,-3,…… と交互に並べて番号をつける。

定理2　N ×N の直積集合の濃度は，0 である。


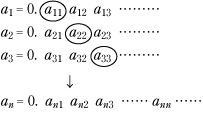
　　この n 行 m 列の番号は，（番）となる。
　よって単射でありかつ全射である。
　　いま，可付番集合 A1，A2，……，An の合併集合は
　　　A1＝{a11，a12，a13，a14，……，a1m，……}
　　　A2＝{a21，a22，a23，a24，……，a2m，……}
　　　　　　　　　　　　　↓
　　　A5＝{a51，a52，a53，a54，……，a5m，……}
　　　An＝{an1，an2，an3，an4，……，anm，……}
　　であるから，上の表と対等である。
　　　0+ 0+ 0+ …… +0 = 0

定理3　有理数 Q の集合は，可付番集合でありその濃度は 0である。
　　　 　
　　これも上記の表と対等である。

定理4（カントールの手法）
　代数方程式 a0xn +a1xn-1+……+an=0（n ∈ N ，a0＞0）の実数解は，つまり代数的数は，可付番集合である。
　この方程式の係数の絶対値和をとり高さと呼ぶ。
　すなわち，n + a0 +｜a1｜+｜a2｜+……+｜an｜
　高さの等しい方程式は有限個しかない。
　高さを一つ h と決めれば，n ＜ h ，a0 ＜h ，｜a1｜＜h ，｜a2｜＜h ，……，｜an｜＜h
　n ，a0 ，a1，a2，……，an の選び方は有限通りに制限される。

　　　高さ2の方程式の実数解　0
　　　高さ3の方程式の実数解　-1，0，1
　　　高さ4の方程式の実数解　-2，-1，- ，0，，1，2

これを最初から並べて

　　0，-1，0，1，-2，-1，- ，0，，1，2，……

同じものを飛ばして，番号をふると，可付番集合であるから，濃度は0である。

　では，実数 R の集合の濃度は，0 であると言えるであろうか。
　数学者カントール（1845〜1918）は実数R は可付番集合ではないことを『対角線論法』を使って証明した。開区間（0，1）の数の集合は可付番集合ではないことを示す。

［証明］（対角線論法） （例）対角線論法）

この，bn は，ann が偶数のときは7を，ann が奇数のときは8とするとbは，a1 からan の数とは異なる。よって，自然数の集合と対等ではない。

この A は，1を加えてずらしている。9のときは1を加えて0とするならば A は1から n の数とは異なる。よって自然数の集合と対等ではない。

　そこで，実数 R の集合の濃度を（アレフ）と定義し，連続体濃度と定義する。
　ここで， を用意して，開区間（0，1）を開区間 に全単射させ，さらに g (x)=tan x を用意し，開区間 を（−∞，+∞）に全単射すれば，合成写像 gf によって開区間（0，1）を（−∞，+∞）という全実数に全単射で写像する。
　
4．連続体仮説（0＜1＜2）
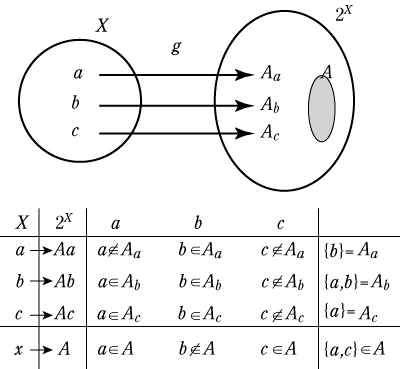
　では，最大濃度は存在するのか，0 と の間に入る濃度 1はあるのか，最小濃度 0であるか？という問いが湧いてくるだろう。
　そこで，集合論では，部分集合の集合を定義し集合族という。
　例えば，X={ a，b，c } の集合の部分集合は，
　　，{ a }，{ b }，{ c }，{ a，b }，{ b，c }，{ c，a }，{ a，b，c }
であったが，集合族とは冪集合で表し，X={ x，y，z } の冪集合は，2X と書いて
　　2X={ ，{ a }，{ b }，{ c }，{ a，b }，{ b，c }，{ c，a }，{ a，b，c }}
となる。
　写像 X →2X は，x →{ x } に対応させると単射であるから，
　　　　　　Card.（ X ）≦Card.（ 2X ）
である。また，この等号は成り立たない。
　つまり，この写像は全射ではない，集合X の冪集合 2X の濃度は，X の濃度より大きい。
　『全射ではない』ことを説明するには，『全射である』と仮定して矛盾を引き出す。a に対応した部分集合Aa（対応のみであり，a が入るというわけではない）と書くことにする。
　　イメージ図

　全射であると仮定して，自分の像になっていない X の要素全体A を用意すると
　　　　　　A={x｜x Ax，x ∈X }
（ア）x ∈A ⇒ x A =g( x )　　よって矛盾
（イ）x A ⇒ x ∈A =g( x )　　よって矛盾
（ア），（イ）より全射ではないということになる。
　また，上の表をみることより，A はAa ，Ab ，Ac と異なっている。（対角線論法）
　この表は，上記に示した『開区間（0，1）の数の集合は可付番集合ではない』ことの証明方法と同じである。
　よって，Card.（ X ）＜Card.（ 2X ）……[1]
となって，最大濃度は存在し，このことから，大きな濃度をもつ集合がつくれることになる。しかし，カントールのパラドックスが起こる。
　『すべての集合 X の部分集合の集合 2X はもはや集合ではない。』

［証明］X を任意の集合とし， 2X を集合とし，X ⊃ 2X ，X ⊂ 2X が成り立つ。
　　　　X = 2X となり [1 ]に矛盾する。　　　(Q. E. D. )

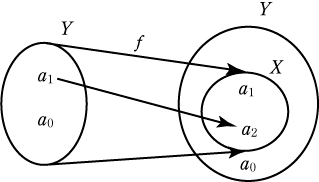
　よって，最大濃度は存在しないことになる。
　このカントールのパラドックスを，ラッセルは次のように説明している。

　ある村に，床屋がいる。自分でそらない村人の男どものひげならば，わしがそる』という命題に対して，床屋が自分のひげは自分でそるとなると，床屋は自分自身でひげをそらないひげをそってやるのだから，床屋は自分自身でひげをそるわけではない。そこで，床屋が自分自身のひげをそらないとすると，床屋は自分自身のひげをそらない人のひげをそってやるのだから自分自身のひげをそってやることになる。よって矛盾を引き起こす。

（ラッセルのパラドックス）

　これは，すべての集合を，自分自身を含まない集合と自分自身を含む集合に分け，すべての集合 A が，自分自身を含まない集合ならばA ∈A より自分自身を含むことになる。すべての集合A が，自分自身を含む集合ならば，A A より自分自身を含まないことになる。矛盾を引き起こす。
　これは，学校で教えている素朴集合論の立場では,矛盾が起きるが，公理的集合論（ZF：ツェルメロ−フレンケル公理系）で規制された公理によって，この問題は回避されている。

　では，最小濃度は0であろうか？次の定理をみてもらいたい。
　　定理　集合 Y がその真部分集合 X と全単射（対等）ならば
　　　　0 = Card.（ Y ）
[証明]

　f : Y →X を全単射とする。真部分集合よりY - X は空でないから，a0∈Y - X となる a0 がある。
　　f (an )=an +1 (n ∈N ) とおくと
　　a1∈ X だから a1≠a0
　f は単射であるから A={ an｜n ∈N } はすべて異なる。
　　g : N →A，g (n )=an
より，A ⊂ Y
　したがって，Card.（ A ）=0 ＜Card.（ Y ）　　　(Q. E. D. )

　　よって，最小濃度は0 である。
　
5．最後に
　生徒独自が数学研究クラブや授業中において『（0，1）の数の個数と（0，3）の数の個数とが、1対1に対応し実数の個数と同じである』ことを見つける場面や代数方程式の解法の歴史やユークリッド幾何学の数学史を紐解くなかで、今一度数学の成り立ちを考える態度である形式主義の流れから論理の形式化を確認しておきたい。

　一般にカントールの予想は、0との間に入る濃度は存在しないというものである。これを『連続体仮説』と呼ぶ。そこで、『任意の無限濃度 n に対して、n ＜ m ＜ 2n となる m は存在するか』が『一般連続体仮説』というが、20＝になるから，n =0であるときの特殊な場合が、この予想である。世界数学者会議でヒルベルトが23の問題を未解決とし20世紀の課題とした。
　我々教師は，今まさに何が現代数学の課題なのかをとらえ，小手先ばかりの大学入試を解くテクニックを研究するのではなく，数学基礎論等を熟読できる能力の養成を考え真面目に真正面から数学を学習し直し，『数学とは何なのか』を考えられる生徒を養成できる教師を目指したい。
　紀元前四千年前の古代オリエントから六千年も経過した今だからこそ，数学史を研究課題として見つける学生達が増えることを願っている。