| 授業実践記録 | |
| 座標系の変換 〜問題を高い位置から見下ろす視野を養う〜 |
|
| (広島)崇徳高等学校 日南休紀彦 |
|
|
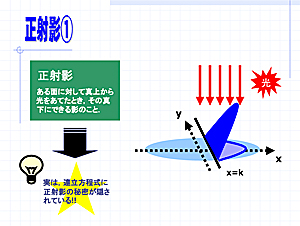
1.はじめに
|
|
|
大学入試問題の出題の意図を探れば,大学レベルの高度な知識を高校レベルに落として出題していることがある.特に,難関校はその傾向が強い.だからこそ高校生から見れば難問に見える. |
|
|
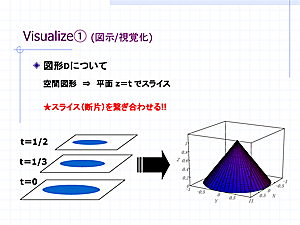
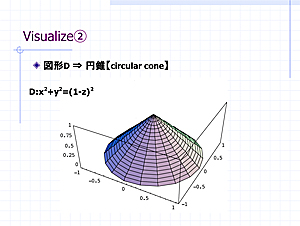
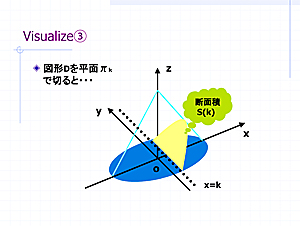
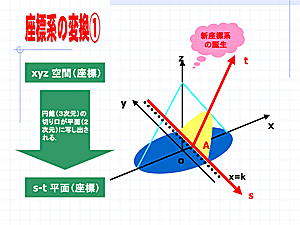
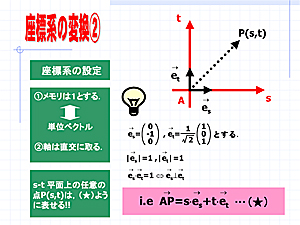
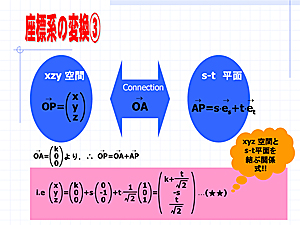
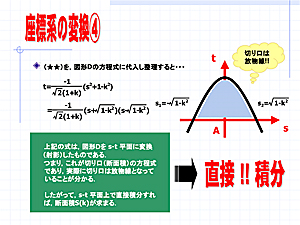
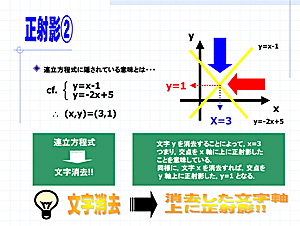
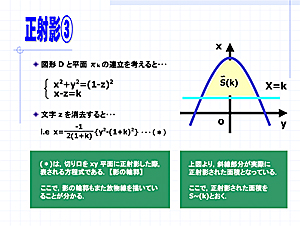
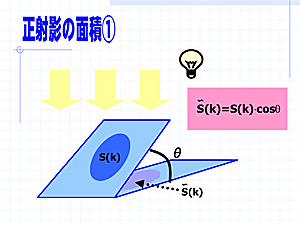
2.実践例
|
|
|