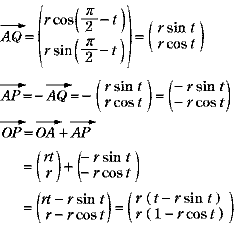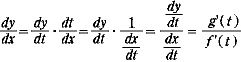[1]曲線の媒介表示の作成(ベクトル方程式を用いて)
高校数学では通常、ベクトルの成分表示を行ベクトル 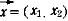 で扱うが、2つ以上のベクトルの和や差を計算する際、列ベクトル で扱うが、2つ以上のベクトルの和や差を計算する際、列ベクトル 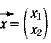 の方が各ベクトルの x 成分、y 成分が捉えやすく計算しやすいことを紹介し、すべて列ベクトルを用いて解説する。また、図の部分は、grapes ソフトを用いてプロジェクターで黒板に投影し、点の軌跡を動的に見させる。時間をかけず効率よく学習できるよう書き込み式にしたプリントを活用する。 の方が各ベクトルの x 成分、y 成分が捉えやすく計算しやすいことを紹介し、すべて列ベクトルを用いて解説する。また、図の部分は、grapes ソフトを用いてプロジェクターで黒板に投影し、点の軌跡を動的に見させる。時間をかけず効率よく学習できるよう書き込み式にしたプリントを活用する。
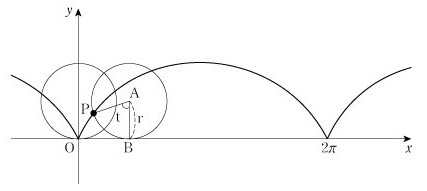
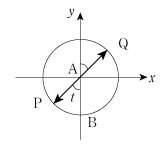
例1 半径 r の円が定直線に接しながら、滑ることなく回転するとき、その円上の定点が描く曲線(サイクロイド)を媒介変数表示する。
解説
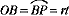 より A(rt,r) より A(rt,r)
よって、 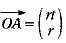
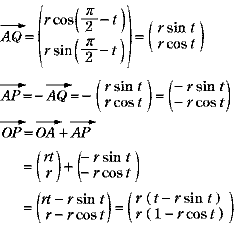
よって、 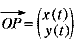 とすると とすると
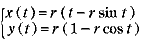
となる。
|
 |
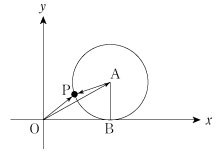 |
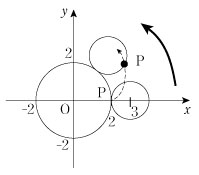
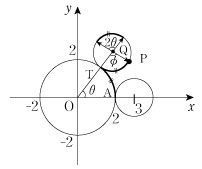
例2 座標平面上に原点 O を中心とする半径2の固定された円 C と、それに外側から接しながら回転する半径1の円 C' がある。円 C' の中心が(3,0)にあるときの円 C' 側の接点に印 P をつけ、円 C' を円 C に接しながら滑らず回転させる。
点 P の描く曲線(外サイクロイド)を媒介変数表示してみる。
解説
右図において、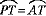 より より 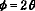
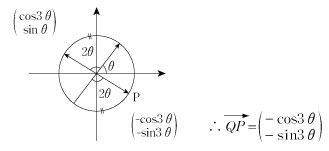
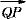 を求めるべく、Qが原点にくるように平行移動すると を求めるべく、Qが原点にくるように平行移動すると
|
 |
 |
よって、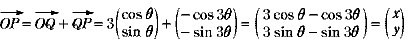
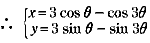
となる。
例2 は練習問題として生徒自身に導かせる。内サイクロイドも考えさせてよかろう。“ベクトル”の概念の利便性を分からせるよき例だと思える。
[2]グラフの周期性および対称性
( I )周期について
「周期は、定期的に同じことが繰り返しされる事象において、任意のある時点の状態に一度循環して戻るまでの期間、時間のことである。」だから、周期(基本周期)が分かると一循環のグラフの概形を捉えるとよい。
●三角関数の基本周期 T について
| 三角関数 |
T |
| y = A sin a (θ+ b ) + c |
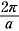 |
| y = A cos a (θ+ b ) + c |
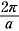 |
| y = A tan a (θ+ b )+ c |
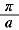 |
●合成関数の基本周期 T について
関数 f ( t ),g ( t ) の基本周期をそれぞれ T1,T2 とする。
合成関数 af ( t )+bg ( t ),f (t) g ( t ) の基本周期 T は
T=min {T12|T12=T1・m=T2・n,(m,n は自然数)}
である。
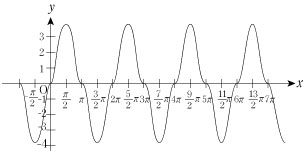
(例)y =3 sin x -sin 3 x の基本周期は 2π
∵ y =sin x の基本周期は 2π、y = sin3 x の基本周期は 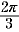 なので なので
基本周期 T は 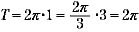 となる。 となる。
y =3 sin x -sin 3 x のグラフ
●媒介変数表示による曲線の周期
曲線 C: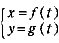
x =f ( t ) の基本周期をTx ,y = g ( t ) の基本周期をTy とすると
曲線 C の基本周期 T は
T=min {Txy|Txy=Tx・m=Ty・n,(m,n は自然数)}
となる。
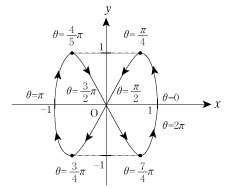
(例) 例2 の曲線
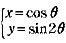 の基本周期は、2π の基本周期は、2π
∵ x =cosθ の基本周期は 2π、y = sin2θ の基本周期は π
よって、基本周期 T は T=2π・1=π・2=2π となる。
曲線 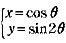 のグラフ のグラフ
( II )グラフの対称性について
●点の対称について
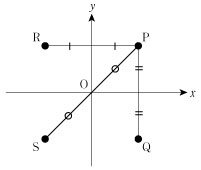
xy 平面上の任意の点 P ( x,y ) について x 軸に関して対称な点を Q 、y 軸に関して対称な点を R 、原点に関して対称な点を S とすると、
Q ( x, - y ),R ( - x,y ),S ( - x, - y )
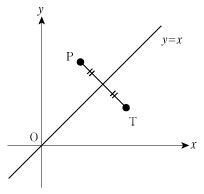
である。また、直線 y = x に関して対称な点を T とすると、
T ( y,x )
である。
●陽関数 y = f ( x ) ,陰関数 F ( x,y )=0 の対称性について
グラフは点の集まりなので、上記の“点の対称”をもとに考える。
|
f ( - x )= f ( x ) を満たすとき、y 軸に関して対称。
(関数 f ( x ) は偶関数)
|
|
f ( - x )= - f ( x ) を満たすとき、原点Oに関して対称。
(関数 f ( x ) は奇関数)
|
|
|
|
F ( - x,y )= F ( x,y ) を満たすとき、y 軸に関して対称。
|
|
F (x, - y )= F ( x,y ) を満たすとき、x 軸に関して対称。
|
|
F (- x, - y )= F ( x,y ) を満たすとき、原点 O に関して対称。
|
●曲線 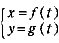 の対称性の調べ方について の対称性の調べ方について
| ( i ) |
x 軸に関して対称であることを示すには、
媒介変数 t の変域内に f (○)=f ( t ) を満たす○を見つけ、
その○が g (○)=- g ( t ) を満たすことを示す。
|
| ( ii ) |
y 軸に関して対称であることを示すには、
媒介変数 t の変域内にg (△) = g ( t ) を満たす△を見つけ、
その△が f (△)=- f ( t ) を満たすことを示す。
|
| ( iii ) |
原点 O に関して対称であることを示すには、
( i ) かつ ( ii ) を示す。
|
| ( iv ) |
直線 y= x に関して対称であることを示すには、
媒介変数 t の変域内に g (◇)=f ( t ) を満たす◇を見つけ、
その◇が f (◇)=g ( t ) を満たすことを示す。
|
(例)
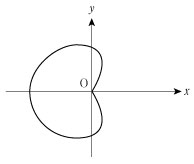
曲線 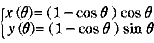 (リマソン曲線)の対称性を調べる。
(リマソン曲線)の対称性を調べる。
〈1〉基本周期は 2π なので、0≦θ≦2π で考えると十分である。
〈2〉x (○) = x (θ) を満たす○を見つける。
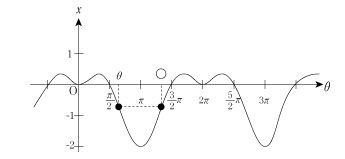
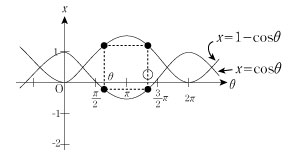
x (θ) = (1- cosθ) cosθ のグラフは上記のようになり、○=2π - θ となるが、このグラフを直感的に捉えるのは難しい。そこで、x (θ)=(1- cosθ)cosθ を構成している 1- cosθ,cosθ について考える。
x =1- cosθ,x =cosθ のグラフは下図のようになる。
よって、グラフより ○=2π- θ が分かる。
〈3〉y (○)=- y (θ) を示す。
y (2π- θ)={1- cos(2π- θ)}sin(2π- θ)
=(1- cosθ){- sinθ}=- (1- cosθ)sinθ=y (θ)
ゆえに、x 軸に関して対称であることが分かった。
[3]増減表及びグラフの概形
関数 y = f ( x ) のグラフの概形は x の値を増加させ、それに伴う y' の符号および y の値を調べることで捉えることができた。
曲線 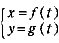 においては媒介変数 t により点 (x,y ) が定まるから媒介変数 t の値を増加させ、それに伴うf ' ( t ),g' ( t ), においては媒介変数 t により点 (x,y ) が定まるから媒介変数 t の値を増加させ、それに伴うf ' ( t ),g' ( t ), 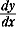 の符号および点 (x,y ) を調べるとよい。 の符号および点 (x,y ) を調べるとよい。
ちなみに、 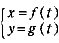 の導関数は合成関数および逆関数の微分法(「数学 III 」)によって の導関数は合成関数および逆関数の微分法(「数学 III 」)によって
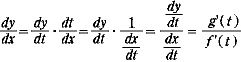
とできる。
(例)再び 例2 の曲線
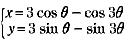 の増減表、グラフの概形 の増減表、グラフの概形
この曲線は、基本周期は 2π で原点に関して対称である。(調べ方は先に述べた。)よって、第1象限にある部分のみを考えるとよいので、x ≧0,y ≧0 より θ の範囲を 0≦θ≦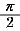 で考える。 で考える。
|
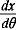 |
= - 3sinθ+3sin3θ= - 3sinθ+3(3sinθ- 4sin3θ)
|
|
|
=6sinθ- 12sin3θ=6sinθ(1 - 2sin2θ)
=6sinθ(1 + 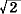 sinθ)(1 - sinθ)(1 - 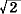 sinθ) sinθ)
|
0≦θ≦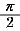 において において 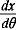 =0 とすると θ=0, =0 とすると θ=0,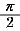
|
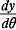 |
=3cosθ - 3cos3θ=3cosθ - 3(- 3cosθ+4cos3θ)
|
|
|
=12cosθ- 12cos3θ=12cosθ(1 - cos2θ)
=12cosθ(1 + cosθ)(1 - cosθ)
|
0≦θ≦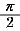 において において 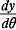 =0 とすると θ=0, =0 とすると θ=0,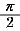
よって、増減表は以下のようになる。
| θ |
0 |
…… |
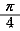 |
…… |
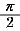 |
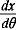 |
0 |
+ |
0 |
ー |
ー |
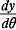 |
0 |
+ |
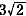 |
+ |
0 |
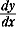 |
 |
+ |
 |
ー |
0 |
| ( x,y ) |
(2,0) |
 |
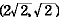 |
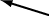 |
(0,4) |
(注)最下段の矢印について
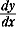 >0 のとき >0 のとき
x の値が左から右へ増加する場合は 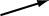
x の値が右から左へ増加する場合は 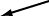
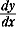 <0 のとき <0 のとき
x の値が左から右へ増加する場合は 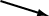
x の値が右から左へ増加する場合は 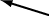
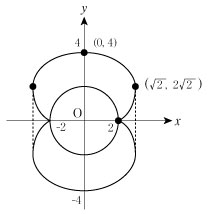
ゆえに、 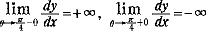 であることと原点に関して対称であることを踏まえてグラフの概形を描くと下図のようになる。 であることと原点に関して対称であることを踏まえてグラフの概形を描くと下図のようになる。
|