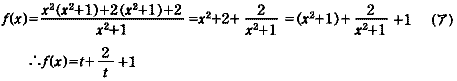授業実践記録
大学入試問題から基礎・基本の指導、
応用・発展の指導を図る工夫
宮崎県立宮崎南高等学校
押方　修
　
1．はじめに

　「教師の資質低下」「学力低下」「理系離れ」が3点セットのように言われているが、ここでは「教師の資質」の一部である「教科指導力」について考えたいと思う。
　私は「教科指導力」とは「教科力」と「指導力」の2つの側面に分けられると考えている。
　「教科力」とは、指導力のバックグラウンドとなる数学的知識、技能、思考力であり、「指導力」とは、教師の備えている数学的見識を、目の前にいる生徒の実態に合わせて授業展開できる学習指導力であると考えている。高校での数学の授業は、この2つの力が相互補完されながら展開されることが理想であると思う。
　最近では学力低下が拍車をかけ、教師の「教科指導力の向上」が早急の課題ともなって、教師の研修も頻繁に行われている。その中では「教科力」と「指導力」を別々に研修している場合が多く、融合的な研修が少ないようにも感じられる。
　「教科指導力」を考えるに当たり、今回は、入試問題をひもとくこと、そしてそれを実際の授業に活かす工夫について紹介してみたい。
　
2．入試問題をひもとく！
【問題1】
　x の2次方程式 x2＋(a-1)x＋a＋2＝0 がある。-2≦ a ≦-1のとき、この2次方程式の実数解 x の取り得る範囲を求めよ。

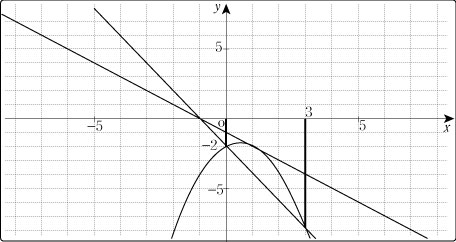
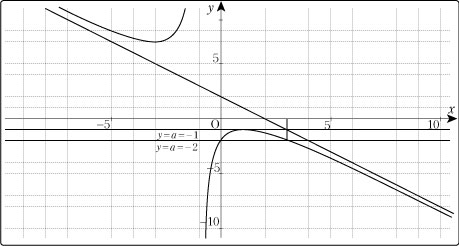
　問題1および以下にあげる問題2はいずれも入試問題であるが、誘導設問を省いて記載している。解法を通して、授業展開につながる内容をまとめてみたい。

●数学 I の範囲での解法〜その1

a について整理して、
　a (x＋1) ＝-x2＋x＋2　から
　y ＝ a (x＋1) ……[1]　と　y＝-x2＋x -2　……[2]
の共有点を考える。
　[1] は、定点（-1，0）を通る直線群である。（ア）
　　　ただし、直線 x＝-1　は除く。（イ）
　　　傾き a において　条件　-2≦a≦-1　から
　　　a ＝-2　のとき [1][2] の共有点のx座標は、x＝0，3
　　　a ＝-1　のとき [1][2] の共有点のx座標は、x＝1
　以上より、共有点は　0≦ x ≦3　に存在する。（図参照）

■指導のポイント

（ア）について…… 変数について整理することの利点。「グラフと方程式」の分野では、x 軸との共有点ばかりが実数解として表現されている。2つのグラフとの共有点としても実数解として捉えられることの確認。
（イ）について…… 定点を通る直線群についての解説とまとめ。
（ウ）について…… 直線の標準形では、表現できない直線が存在することの解説とまとめ。

●数学 I での解法〜その2

a について、解くと
　(x＋1)a＝ - x2＋x - 2
　　　x＝-1 のとき　与式は成立しない。　（ア）
　　　x≠-1 のとき　
　　　-2≦ a ≦-1 より　

　両辺に (x＋1)2＞0を掛けて　（イ）
　　　-2 (x＋1)2≦-x2＋x - 2≦- (x＋1)2　（ウ）
　これを解いて、0≦ x ≦3

■指導のポイント

（ア）について…… 文字および文字式で割り算するときの場合分けの確認。
（イ）について…… 分数式で表された不等式の解法とまとめ。
（ウ）について…… 連立2次不等式の解法とまとめ。

●数学 III での解法〜その1

aについて、解くと
　(x＋1)a＝-x2＋x - 2
　　x＝-1のとき　与式は成立しない。[1]
　　x≠-1のとき　から
　　y＝a と との共有点について考える。
　　 のグラフは
　　　　のとき　 x＝-3，1（増減表省略）
　　　　から　漸近線　y＝-x＋2，y＝-1
　　y＝a（-2≦a≦-1）との共通点は、
　　　　a＝-2 のとき　 x＝0，3　　a＝-1 のとき　 x＝1　から
　　ゆえに 0≦x≦3

■指導のポイント
　数学 III の既習済みの生徒において、この問題の演習を行った場合、変数分離を行い、確定されるグラフと変化する直線との共有点についての考察となることが多い。
　しかしながら、x についての2次方程式であることに着目させることで、数学 I の範囲での解法を示すことができる。

　また、別解として

判別式を D とすると、実数解をもつことから D ≧0より
D ＝(a - 1)2-4(a＋2)≧0 ⇔ a2-6a -7≧0 ⇔ (a -7)(a＋1)≧0 ⇔ a≦-1，7≦a
このとき
から x を a の関数と考え、
定義域 -2≦ a ≦-1 における x の範囲を考える。

という解法も考えられる。しかし微分の練習にはなることはあっても、勧められる解法とはいえない。

【問題2】
　x が実数のとき、の最小値を求めよ

　数学 III の既習済みであれば、すぐ微分、増減、最小値という解法になろうが、以下の誘導設問があれば、解法も変化してくる。

(1)　t ＝ x2＋1 とおくとき、f (x) を t で表せ。

　　　

(2)　f (x) の最小値を求めよ。
　　　t ＝ x2＋1＞0　より　＞0 から　相加平均・相乗平均の関係から
　　　
　　　よって、最小値　

　入試問題も誘導設問があるとないとでは、難易度が大きく変化する。ある程度演習をつんだあとから、誘導問題をはずした問題を作成し、その問題で解答づくりができるようになると数学の力はより深まる。

　さて、この問題には、いろいろな出題方法が考えられる。その一つは、下記の問いかけであろうか。

x が実数のとき、を証明せよ。

　私は、よく問題の言い回しを変えたり、問いかけを変えたりしながら問題を読むことが多い。変化していく問題の問いかけに、解法自体はあまり変化しないことに興味をそそられている生徒も少なくない。
　
3．おわりに

　「教科力」の中には、入試問題を解法する力も必要である。しかし、授業では入試を意識した内容を、どの段階で、どのように指導するかが鍵となる。それが「指導力」である。バランスの良い授業を展開したいと思う。

　私は、問題演習では次の2点を生徒へ呼びかけている。

（1） 問題作成者の意図する事柄を読み取ることができると問題解法はおもしろくなる。
（2） 誘導設問を考えないで、いきなり最終設問が解けるかな。

　入試問題を基礎・基本まで細分化するのもおもしろい。また発展・応用まで変化させるのもおもしろい。そして生徒が数学をおもしろいと思うようになることがおもしろい。
　この機会を与えていただいた啓林館の方に感謝いたします。