授業実践記録
「ハノイの塔」の謎に迫る
（佐賀）龍谷高等学校
中島一明
　
1.　はじめに
　本校では夏休みを利用して、中学3年生を対象に一日体験入学を毎年実施している。その中で40分ほどの模擬授業を行うことになっている。中学生に高校の学習内容の一端を楽しく学んでもらうために、題材を考えるときはいささか気をつかう。
　そこで、今年度は数学パズルの「ハノイの塔」を取り扱うことにした。「ハノイの塔」は数列との関連性が深く、高校に入ってから漸化式や数学的帰納法を理解するのに有効な教材と思われる。
　
2.　ハノイの塔
　「ハノイの塔」は、フランスの数学者 E・リュカ（Edouard Lucas）が1883年に考えたものである。リュカは、インドに次のような伝説があると説明している。
　インドのガンジス河の畔のヴァラナシにある大寺院には、3つの塔（ダイヤモンドの針）があった。そのうち1本には、64枚の黄金の円盤が大きい円盤を下にして順に重ねられていたという。バラモン僧たちはそこで、一日中円盤を別の柱に移しかえる作業を行っている。そして、全ての円盤の移しかえが終わったときに、この世は崩壊し終焉を迎える。

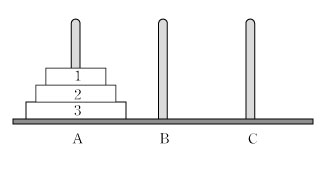
　64枚では多いので、3枚で実験してみる。AからCに移すことを考える。ルールは、次の3つで、最少の手数を求めたい。
　　[1] 1回に1枚ずつどれかの杭に移動させることができる。
　　[2] 小さな円盤の上には大きな円盤をのせることはできない。
　　[3] 補助として B を用いてもよい。
　
3.　解き方

　3本の杭に A、B、C の名前を付ける。最初Aに3個の円盤があり、次のようにCにすべての円盤を移動させる。

　　　[1] 円盤1を A から C に移動する。
　　　[2] 円盤2を A から B に移動する。
　　　[3] 円盤1を C から B に移動する。
　　　[4] 円盤3を A から C に移動する。
　　　[5] 円盤1を B から A に移動する。
　　　[6] 円盤2を B から C に移動する。
　　　[7] 円盤1を A から C に移動する。

よって、円盤が3枚のときの最少の手数は7回ということになる。

　さらに、円盤の枚数を変えて、一般化していく。
　　　円盤が1枚のとき、最少の手数は1回
　　　円盤が2枚のとき、最少の手数は3回
　　　円盤が3枚のとき、最少の手数は7回
　　　円盤が4枚のとき、最少の手数は15回
　　　円盤が5枚のとき、最少の手数は31回
　　　　　・・・・・・・・・・
　　　円盤が n 枚のとき、最少の手数は an 回

《階差数列で求める》
　n 枚の円盤を A から C に移動させる最少の手数をan 回とする。
　　　　　　　　　｛an｝：1、3、7、15、31、・・・
数列｛an｝の階差数列｛bn｝をとると、
　　　　　　　　　｛bn｝：2、4、8、16、・・・
数列｛bn｝は、初項2、公比2の等比数列になるから、bn=2・2n-1=2n
　n ≧2 のとき、
　n =1のとき、a1=21-1=1のときも成り立つ。
よって、an =2n-1 である。

《漸化式をつくって求める》
　n 枚の円盤を A から C に移動させる最少の手数を an 回とする。円盤が1枚のときは、最少の手数は1回である。次に、円盤が n＋1枚のときを考える。n＋1枚の円盤を A から C まで移動させるには、まず n 枚の円盤を A から B に移動させて、n＋1枚目の円盤を A から C に移動させる。さらに、B にある n 枚の円盤を C に移動させればよい。つまり、an+1=an+1+an から、次の関係式は成り立つ。

　　　　　a1=1、an+1=2an+1

　両辺にそれぞれ1を加えると、an+1=2(an+1)
数列｛an＋1｝は、初項 a1＋1=2、公比2の等比数列だから、an+1=2・2n-1
　よって、an =2n-1である。

　したがって、64枚の円盤を移動させるには、最少で 264-1回の手数が必要になる。
　
4.　実際には
　ハノイの塔の伝説を思い出してください。64枚の黄金の円盤が全ての円盤の移しかえが終わったときに、この世は崩壊し終焉を迎えるという伝説です。円盤を1枚移動させるのに1秒かかったとして、この世が崩壊するのに要する時間を計算してみる。実際に、264-1（秒）を計算すればよいことになる。

《直接計算して求める》
264-1 = 18446744073709551615（秒）
= 18446744073709551615÷60÷60÷24÷365（年）
≒ 5849（億年）

《対数計算で求める》
　P=264-1 とおく。P＋1=264 の両辺の常用対数をとると、
log10(P + 1) = log10264
= 64 log102
　　常用対数表より、log102≒0.3010 だから
log10(P + 1) ≒ 19.264
P+1 ≒ 1019.264
P ≒ 1019.264-1
≒ 1019.264
= 1019×100.264（秒）

　ここで、y = log10x は単調に増加する関数であり、 log101.83=0.2625、log101.84=0.2648、log101.85=0.2672 だから、100.264≒1.84 とみなすと、P ≒1.84×1019（秒）≒5835（億年）

　「ハノイの塔」の話はリュカの作った架空の話だが、1枚を移動させるのに1秒かかったとして、64枚の円盤を移動させるには、最短でも約5800億年かかる。地球が誕生してから今まで約46億年、宇宙誕生は百数十億年前と考えられているから、この世が崩壊し終焉を迎える心配はないということになる。

参考『数学浪漫塾』（仙田章雄　弘文堂2000）
　
5.　最後に

　「ハノイの塔」の問題の中にはまだまだ解明されていない性質や法則があるような感じがする。「ハノイの塔」の謎を完全に解くことはできなかったが、その謎に少しでも迫ることができたのではないかと思っている。この問題を解く中で、何か知的好奇心を刺激され、楽しいひとときを過ごすことができた。
　最後に、一日体験入学の中で、模擬授業を受けた中学生の感想を紹介したいと思う。
　今日はゲーム感覚で考えていったのでとても楽しく学べました。また、ゲームの結果をいろいろな視点から見てみると、いろいろな事が分かってきて興味深かったです。／やっぱり中学校の問題より高校の方が複雑で手応えがあるので楽しかった。／考えたことはとても難しい内容だったけど、とてもおもしろかった。こんな楽しくて、わかりやすい内容だったら毎日でもやりたい。／だんだん規則性が分かってきた。やっぱり数学は面白い。／とても難しかったです。どういう法則があるのかを見つけ出すのが一苦労でした。／ハノイの塔を少々甘く考えていたが、数学はなかなか奥が深い。／ハノイの塔は全く聞いたことがなかったが、規則性を見つけることが楽しかった。／実際に厚紙を使って考えたのがわかりやすかった。