| 授業実践記録 | |
| 「無限小量とは何か」の問いに答えて |
|
| 武蔵工業大学付属高等学校 田口哲夫 |
|
|
|
1.はじめに
|
|
| 大学の授業において,微分積分における収束発散の議論は,εーδ論法でなされ,高校においても微分積分は,『直感的に理解しておけ』など,意味をもたせずに dy は『単なる記号』,さらには,dy/dx (ディy ディx と読む) は有限確定値の極限値であるから dy と dx で切り離すことはできないと教えている先生も多い. その後,いくつかの計算,特に逆関数の微分ではあたかも分数のように計算し,置換積分において dy と dx は無理矢理切り離され生徒は記号の魔術にかかり『計算の結果さえあたればよいという』大胆な生徒も出現してくる.このことで,本来の数学教育が崩壊していくはめにある.ここに,自然現象を捉える学生への解析学の基本定理である無限小解析をオイラーにならって導入してみよう.まさに,高校生の数学IIIC の授業において,微分積分の想像をかき立てる局所的性質を納得するのに,直感的量の無限小量を考え無限小解析を導入する試みである. |
|
|
2.無限小超実数の定義導入
|
|
| あらゆる正の実数 r に対して,|ε| < r が成り立つとき,εを無限小超実数と呼ぶ. 注)ある実数 r に対して |ε| < r が成り立つとき,εを有限超実数と呼ぶ.さらに,どんな実数に対しても |ε| > r となるとき,εを無限大超実数と呼ぶ. 二つの超実数 x, y に対し,xーy が無限小のとき, xと y は無限に近いと言い,x と定義する.よって,無限小超実数と無限小超実数との比が極限であると定義される. さて,関数の勾配を無限小顕微鏡でみることにしょう.
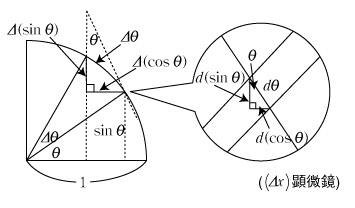
曲線と接線とは,焦点 (a, f (a)) のΔx 無限小顕微鏡では識別することはできないが,焦点 (a+Δx, f (a+Δx )) の (Δx )2 無限小顕微鏡でみれば誤差が識別できる.つまり勾配 S の直線と y= f (x) とは平行に見える. であるから
|
|
|
3. 微分dy(ディy)(differental)の計算公式
|
|
| p,q,r,s を変化量,a を定量とおく. (1)da = 0(定量は変化しない量) (2)q = ap を微分すると,dq = a (p+dp) ーap =a dp (3)d (p + q + r + s +…) = dp + dq + dr + ds +…(線形性) (4)u = pq を微分すると, du = (p + du) (q + dq) ー pq = pdq + adp + dpdq = pdq + adp (dpdq は dp,dq に対して高位の無限小) (5) 例(4)を利用して以下のような計算となる. dx の2次以上の項は高位の無限小より 対数関数や指数関数や合成関数についても上の公式を利用され,このような計算が本来,微分計算と呼ぶことになる. さて,近似式(テーラー展開)からの導入では高校では一般に次のように導入しているであろう. |
|
|
4.無限小解析を授業展開
|
|
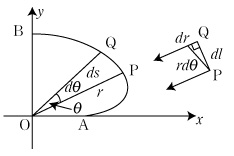
| 例1 無限小解析を導入するには,カージオイドやレムニスケートの面積 や弧長を極座標で求めるのが最も一般的である. カージオイドに対して 極座標では,r (θ) = 1+ cosθである.
(Δx) 無限小望遠鏡を利用し,図形 OPQ を扇形 OPQ と見て, 例2 山口大学理学部数理学科の2001年の問題である.
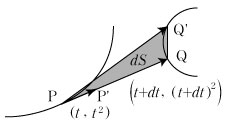
dt 秒後に, ところで, |
|
|
5.終わりに
|
|
| 高校数学から,一次変換,微分方程式が消え,『線形性』『変数分離形』『同次形』という難解な言葉が教科書や参考書からなくなってから十数年が経過した.微分のもつ本来の瞬間的な意味も強調されなくなり,さらに,大学入試では数学 II ・Bまでの範囲で受験する生徒やAO入試学生も増える中,『置換積分』『部分積分』の計算すら完全に解答できない生徒も急速に増えている. これは,我々教師が数学の微分積分の分野でしか捉えることのできない『無限小の世界』を無視して,極限や計算力に対する詰め込み知識しか学生に与えてこなかったからであろう.工学や理学者での利用する立場から現象をもう一度考えなおすべき時期にきていると感じる.高校生に特に想像をかき立てる,数学者コーシー以前の『オイラーの無限小解析』にもどって講議することこそ大切ではないか. 特に,無限小超実数の定義や,例題1,2で無限小量を利用するときの間違いやすい点,さらに,オイラーの微分は大学1年次の『全微分』につながっていくことを強調しておきたい. 教科書を早く終わらせることに周知して大学入試のためのパターン問題演習に入るといった高校も今後増えていく一方にある中,『εーδ論法』とはいかないまでも,局所的解析を納得させる授業技術を心掛けていかなければならないと思う昨今である. [参考文献] 1,dx と dy の解析学 高瀬正仁著 2,無限小解析の基礎 キースラー著 齋藤正彦訳 |
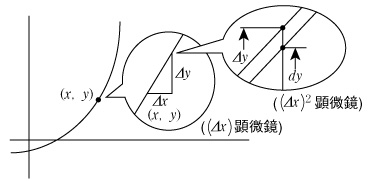
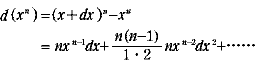
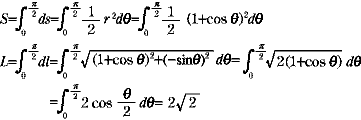
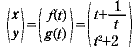
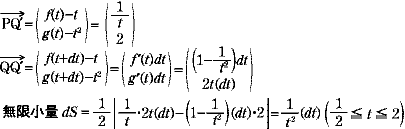
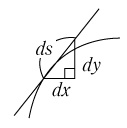 例3 レムニスケートの弧長をオイラーの微分にならって計算してみよう.
例3 レムニスケートの弧長をオイラーの微分にならって計算してみよう.