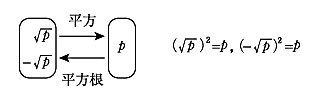授業実践記録
数学教育と理解について
「数学 I 」　数と式を題材に
（広島）安田女子中高等学校
井上栄二
　
1．はじめに
　本校が65分授業を始めて2年目に入っている。このためパソコンやビデオの使えるプロジェクターを全教室に導入し，小テストの実施など，充実した授業への取り組みを強化している。
　数学教育においてもいろいろな取り組みを行っているが，生徒に思考力や判断力を身につけさせるとともに，生徒の「わかる」「わからない」という反応を大切にしていきたいと考えている。そして，「わかる」という理解についても，もっと教師の意識を明確にしておくべきだと考える。これが今，私にとっての，授業を進める上での課題である。
　この課題への取り組みとして，「理解」についての２つの研究を紹介し，これに基づいて，数学Ⅰの実践方法を考察し，レポートをまとめてみようと思う。
　
2．「理解」への研究
　私が学んだ「理解（understanding）」の研究は次の2つである。
（1）認知説による理解－スケンプ氏（Skemp.R.R）の理解
　スケンプ氏は，理解を次の3つに分類した。
・用具的理解…… 記憶している規則を機械的に（理由は知らないままに）応用する能力
・関係的理解…… 一般的な数学的関係から特殊な規則や手続きを引き出せる能力
・形式的理解…… 論理的理解
　さらに彼は，理解の「質」に言及している。1つの規則を適用することと，2つの規則を結合することは，別な心的機構を通じて行われると考え，最初の心的機構をΔ1，後者，つまり，いくつかの規則を目的に合うように結合する心的機構をΔ2とした。そしてΔ1だけで行われる活動（直観的様式の理解）と，Δ2によってΔ1を制御しながら行われる，より高次の活動（反省的様式の理解）があるわけである。

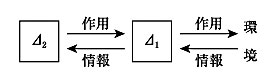
（2）連合説による理解－ヘイロック氏（D.W.Haylock）の理解
　ヘイロック氏は，理解を「何かを理解するとは（認知的な）つながりをつくることである」と捉えている。したがって，より多くのつながりをつくればつくるほどより深く理解されたということになるわけである。そして氏は，生徒があることを理解したか否かは生徒がつながりをつくったことを示す数学的活動で判断されるとし，その数学的行動のパターンは，つながりをつくる際に用いる4つの要素

E1　言語 E2　具体的場面
E3　絵・図 E4　記号

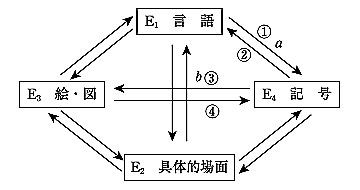
に着目すると，つながりはそれらの相互間でつけられるので，次の図の示すように，全部で12種類に分けられるとしている。

　この図で，a は言語と記号のつながりを表し，a－①は，言語から記号へのつながりをつくる（例：2乗して正の数 p になる数を p の平方根といい，正の方を ，負の方を で表すのは a－①の例，下の図は b－④ の例である）ことを表している。このように氏の考えは「あることを理解させる場合の指導の手だてを考える具体的視点を提供するとともに，理解させることができたか否かが学習者の行為によって判断できるようにもなっている」ことに特色がある。
　
3．授業への応用－数学 I　数と式において
　2.で2氏の理解の研究の概略をみたが，私は，数学 I 数と式の単元をすべて，次のような理解の分類にあてはめてみた。

[1]用具的理解か関係的理解か
[2]心的機構はΔ1かΔ2
[3]ヘイロック氏の12種類のつながりのどれか

　また，[1]，[2]は用具的理解，関係的理解 の4種類のどれかというところまで考えた。私はこれらの分類を，次のように授業に応用した。
[ア] 教科書等の説明には，Δ1，Δ2を意識して応用した。
[イ] 生徒の活動には，12種類の「つながり」をつくることを意識して応用した。
[ウ] 用具的理解でも「つながり」をつくることを重視した。

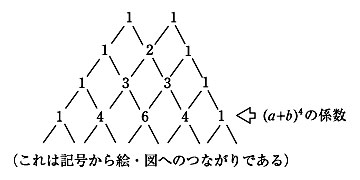
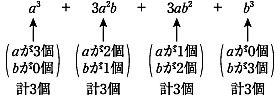
〈乗法公式 (a±b)3の指導例〉
　説明については，関係的理解が深まるようにつとめた。(a＋b)3=a3＋3a2b＋3ab2＋b3を乗法公式として覚えさせるだけでなく，次のように何段階にも分けて指導した。

（i） (a＋b)3=(a＋b)(a＋b)2として公式を導く。
（ii） (a＋b)1=a＋b
(a＋b)2=a2＋2ab＋b2
(a＋b)3=a3＋3a2b＋3ab2＋b3
から，係数をとり出し，「パスカルの三角形」を指導した。
（iii） また，文字の方でも次の規則を発見させた。

つまりすべての項で文字は3個であることである。次の段階で，ヘイロック氏のつながりやΔ2とも関連して練習を進める。
　文字の変更 (x＋y)3＝x3＋3x2y＋3xy2＋y3
　項の変更 (2x＋y)3＝(2x)3＋3(2x)2y＋3(2x)y2＋y3
次に(a－b)3については，(a＋b)3の場合と同じΔ1での計算：(a－b)3＝(a－b)(a－b)2と，
Δ2として，(a－b)3＝
＝
＝
 {a＋(－b)}3
a3＋3a2(－b)＋3a(－b)2＋(－b)3
a3－3a2b＋3ab2－b3
のように(a＋b)3の公式に適用させる。この計算を入れると，bの指数が奇数のとき符号が－になることがわかる。最後に，
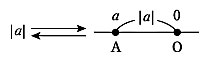
　　(a±b)3=a3±3a2b＋3ab2±b3（複号同順）
としてこの教材の指導を終えた。
〈絶対値の指導例〉
　絶対値の記号 は指導が難しいものの一つである。ここでは，あまり関係的理解を求めない方がよさそうである。例えば では， [1] a，b のどちらかが 0，[2] a＞0，b＞0，[3] a＞0，b＜0，[4] a＜0，b＜0などに場合分けして説明するより，具体的に a＝－2，b＝3 として計算させた方がヘイロック氏のいう具体的場面から記号へのつながりが有効となるであろう。
　絶対値の定義，性質も，言語，記号，絵・図，具体的場面の間のつながりをつくってみせる方がわかりやすいと考える。
　
4．おわりに
　以上，理解の研究を意識した授業展開を実践してきて、具体例を少し述べた。これらの実践でわかったことを次にあげる。
　[1] 関係的理解を重視すること
　[2] Δ2の指導は，よりていねいにすること
　[3] ヘイロック氏の「つながり」の指導において，必ず逆のつながりを指導すること。また，1つの教材においてできるだけ多くのつながりをつくらせること。
　平成14年11月放送のNHK教育フォーカスの番組でも，どんなときに授業に対してやる気になるかという国立教育研究所の調査では，1．授業がよくわかるとき，2．授業が面白いとき，3．将来つきたい職業に関心を持ったとき，とあり，やはり1番目に「わかる授業」をやる気の第1因にしている。
　「わかる授業」を目指して，全体を見渡す説明には主としてスケンプ氏の理解を，いろいろな事柄を構造的に結びつけるために，ヘイロック氏の（「つながりをつくる」）理解を活用していきたい。

引用・参考文献
1.子どもの理解を深める教材の開発（石田忠男）
2.『数学理解の認知科学』（R.B.デーヴィス　佐伯胖監訳）国土社