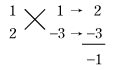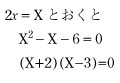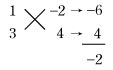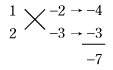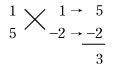授業実践記録
2次方程式（因数分解による解法）
和歌山県立日高高等学校
辻本純一
　
1．はじめに
　2次方程式の解法と因数分解とは関係が深い。解の公式を学ぶ前に，因数分解を利用した解法について学習させたい。
　さらに，いろいろな問題の解を求めるために，2次方程式を作り，解くことを考えさせる。
　
2．2次方程式と因数分解
　実数に関する性質
　　ab＝0　⇔　a＝0　または　b＝0
を利用して，2次方程式の解を求めてみよう。

例1　2次方程式　x2−x−6＝0を解け。
　　左辺を因数分解して，(x＋2)(x−3)＝0
　　よって，x＝−2，3

例2　2次方程式　2x2−x−3＝0を解け。
　　左辺を因数分解して，(x＋1)(2x−3)＝0
　　よって，x＝−1，

　例2では，たすきがけによらない解法がある。

　例2の方程式の両辺に2をかけると，

　　4x2−2x−6＝0
　　(2x)2−(2x)−6＝0
　　(2x＋2)(2x−3)＝0
　　よって，x＝−1，

例3　2次方程式　−x2＋3x＋10＝0を解け。
　　両辺に−1をかけて，x2−3ｘ−10＝0
　　(x＋2)(x−5)＝0
　　よって，x＝−2，5

例4　2次方程式　x2−x−4＝0を解け。
　　両辺に2をかけて，3x2−2 x−8＝0
　　(x−2)(3 x＋4)＝0
　　よって，x＝2，
例5　2次方程式　0.2 x2−0.7 x＋0.6＝0を解け。
　　両辺に10をかけて，2 x2−7x＋6＝0
　　(x−2)(2 x−3)＝0
　　よって，x＝2，

　例3，例4，例5では，各係数をすべて整数で，x2の係数を正にするように，方程式の両辺に定数をかけている。そうすることによって，整数を係数とする1次式の積に因数分解できている。

例6　2次方程式　20x2＋12x−8＝0を解け。
　　両辺を4で割って，5x2＋3 x−2＝0
　　(x＋1)(5 x−2)＝0
　　よって，x＝−1，

　例6では，両辺を4で割らずに左辺を因数分解すると，
　　(4 x＋4)(5 x−2)＝0，(2 x＋2)(10 x−4)＝0，
　　(x＋1)(20 x−8)＝0
のように，いろいろな計算が考えられる。
　そこで，整数を係数とする2次方程式においては，各係数の最大公約数が1になるように計算すると，因数分解が少しは簡単になる。
　
3．２次方程式の利用
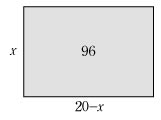
　2次方程式を利用して解くことのできる問題を扱う。

例7　隣り合う2辺の和が20の長方形の面積が96である。このとき2辺の長さ
　を求めよ。

[解]　1辺の長さをxとすると，他の辺の長さは
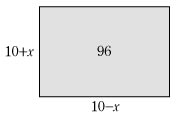
　20−x である。
　　面積が96だから，x(20−x)＝96
　　x2−20x＋96＝0
　　(x−8)(x−12)＝0
　　よって，x＝8，12
　　求める2辺の長さは，8と12である。

　例7では，求めたい辺の長さの1つをxとおいて，2辺の長さの和が20であることから，もう1つの辺の長さを20−x とした。
　この問題において，文字xを何にするかで，その解法が違ったものになる。そこで，次のような別解をあげておく。
[別解]　長方形の隣り合う2辺の長さを10＋x，
　10−x とする。
　　面積が96だから，(10＋x)(10−x)＝96
　　100−x2＝96
　　x2＝4
　　よって，x＝±2
　　求める2辺の長さは，8と12である。

(注) [別解] の考え方から，2辺の長さの和が20の長方形の面積は，
　　(10＋x)(10−x)＝100−x2
と表すことができる。そして，この式から，x＝0，つまり，1辺の長さが10の正方形のとき，その面積は最大になることがわかる。
　
4．おわりに
　2次方程式の解の公式を学ぶと，どんな2次方程式でも公式を使って解を求める生徒がいる。そこで，2次方程式を解くときは，まず因数分解できるかどうかを考えるようにしたい。