●図形の性質と証明No.４
【1】平行四辺形の性質
| テーマ |
： |
平行四辺形のいろいろな性質を見つけ，証明していきます。 |
〔定義〕
| ・ |
四角形の向かい合う辺を( )，向かい合う角を( )という。
|
| ・ |
２組の対辺がそれぞれ( )な四角形を，平行四辺形という。
|
| 〔平行四辺形の性質１〕平行四辺形ならば( )はそれぞれ等しい。 |
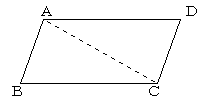
〔証明〕対角線ACをひく。←補助線
△ABCと△CDAにおいて
平行線の錯角は等しいから
| |
∠BAC＝∠( ) |
・・・[1] |
| |
∠( )＝∠DAC |
・・・[2] |
| |
また( ) |
・・・[3] |
|
|
[1]，[2]，[3]より( )から
△ABC≡△CDA
したがって AB＝CD，AD＝CB
|
| 〔平行四辺形の性質２〕平行四辺形ならば( )はそれぞれ等しい。 |
〔証明〕
[3]の △ABC≡△CDAより
| |
∠B＝∠( ) |
・・・[4] |
| また |
∠BAD＝∠( )＋∠( ) |
・・・[5] |
| |
∠BCD＝∠( )＋∠( ） |
・・・[6] |
| [1]，[2]，[5]，[6]より ∠BAD＝∠BCD |
〔別の証明〕
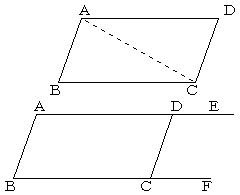
辺ADの延長上に点Eを
辺BCの延長上に点Fをとる。
平行線の同位角・錯角は等しいから |
| |
∠A＝∠( )＝∠( ) |
|
| |
∠B＝∠( )＝∠( ) |
|
|
|
| 〔平行四辺形の性質３〕平行四辺形ならば( ) |
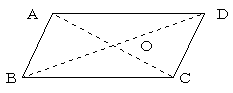
〔証明〕 ABCDで，対角線ACとBDの交点をOとする。
△ABOと△( )において
平行四辺形の対辺は等しいから
| |
( )＝( ) |
・・・[1] |
| 平行線の錯角は等しいから |
| |
∠( )＝∠( ) |
・・・[2] |
| |
∠( )＝∠( ) |
・・・[3] |
|
|
[1]，[2]，[3]より( )から△ABO≡△( )
したがってOA＝( )，OB＝( )
|
〔平行四辺形の性質を利用した証明問題〕
ABCDの対角線BD上に，BE＝DFとなるように２点E，Fをとる。 |
(図)
|
| （１） |
問題にあう図を書きなさい。  |
| （２） |
AEとCFの間にはどのような関係があるか予想を立て，証明しなさい。 |
| （３） |
点E，Fの取り方を変えて，オリジナル問題を考えよう。 |
|
|
