●図形の性質と証明No.2
〔復習〕二等辺三角形の性質
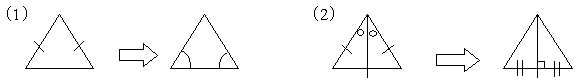 |
右の△ABCで∠B=∠Cとする。
頂角∠Aの二等分線をひき,
底辺BCとの交点をDとする。
△( )と△( )において,
| 図から, |
( ) |
・・・[1] |
| 仮定から, |
( )=( ) |
・・・[2] |
|
ADは∠Aの二等分線だから,
|
| |
( )=( ) |
・・・[3] |
|
三角形の内角の和は180°だから,
|
| ∠ADB=180°−(∠ +∠ ) |
・・・[4] |
| ∠ADC=180°−(∠ +∠ ) |
・・・[5] |
| [2],[3],[4],[5]より ∠( )=∠( ) |
・・・[6] |
|
|
( ),( ),( )より( )から△( )≡△( )
( )からAB=AC |
| |
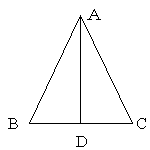
〔定理〕(二等辺三角形になるための条件) |
|
| |
|
三角形の2角が等しければ
その三角形は等しい2角を( )とする二等辺三角形である。
|
|
| ☆ |
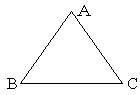
『3つの角が等しい三角形は正三角形である』こと,つまり,
『△ABCで∠A=∠B=∠CならばAB=BC=CAとなる』
ことを証明しなさい。
〔証明〕
|
 |
|