授業実践記録（数学）
自発的思考活動のための授業改善の工夫
１．実践の内容
今年度は３学年数学ⅠAⅡB演習，数学Ⅲを担当している。特に文系の演習の授業を通して感じることは，多少できる生徒であってもその問題固有の解法として覚えているだけのことが多い，ということ。したがって，自分の理解の仕方を自分の言葉で表現することや，さらに考えを発展させたり深めていくこともない。我々が授業を計画する際，この点にどう切り込むか？が問題である。その際の一つの指針とされているのが学習指導要領で言われる「言語活動」であろう。
生徒自身が考えを発展させたり深めたりする自発的思考活動を始めるには，まずはそのきっかけとなるような活動経験と，考える力を育む理解の仕方が必要である。そこで，思考力，判断力，表現力を働かせるきっかけとなる活動を取り入れた授業改善を試みた。
２．教科書（問題集）での取り扱いと授業改善の工夫
形式的操作の学習に陥りやすく，本来の理解を得られていないために生徒の学習活動に発展性が見られない内容を選定し指導の工夫を考えた。
① 実践「領域と最大・最小」
領域D内の点（x，y）に対してx+yの最大値・最小値を求める問題。教科書では，「x+y=k とおくと，これは傾きが‐1, y切片が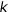
の直線を表す。よって，この直線が領域
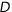と共有点をもつような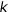の値の最大値，最小値を求めればよい」とある。 生徒たちは，何故直線の問題になったのか？ 直線が領域Dと共有点をもつようなとはどういうことなのか？ といった疑問を持つ。しかし問題を解くために注意を払う（払わされる）のは，直線の傾きと領域との共有点の有無であって，最も重要な点への意識は低い。
＜授業改善の工夫のポイント＞ きちんと点と領域を意識させる工夫をする。
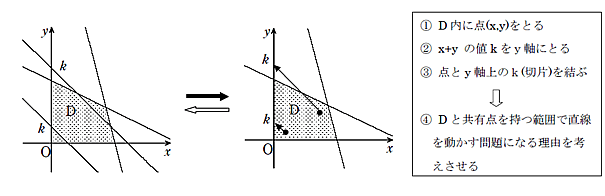
[生徒の様子]
- ・すでにこのタイプの問題に慣れてしまっている生徒でも，「そういうことだったのか」という反応を見せる場合が多い。そしてあらためて問題を読み返し，一つ一つ与えられた条件の意味を考え始める。その後，ようやく結果的に直線を領域と共有点を持つ範囲で動かしたときのy切片を考えればよいことを納得する。
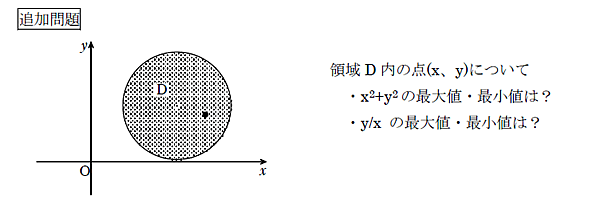
- ・例題にならって，=kとしたときのkの表す図形的意味(２点間の距離２，円の半径２，直線の傾き)を言い表すことができればその後の解決は早い。そして必ず「ここの点のとき…」という説明ができるようになる。なんだか訳も分からず直線を上下させギリギリの場面を“答え”としていたときとは，理解の仕方は異なり，学習の発展性に期待ができると感じた。
② 実践「三角関数の合成」
教科書では「asinθ+bcosθの変形」としてこの内容が扱われている。平方完成と同じような扱いであり，関数の最大値・最小値を求める問題や三角方程式・不等式を解くために便利な変形方法といった感じである。この内容が含む身近な現象を連想させることはない。加法定理を逆にたどって変形するその方法は，多くの生徒にとって技巧的であり唐突な印象を持つようである。その原因と考えられるのは，加法定理の持つ“波の分解”という働きを伝えていないことが考えられる。そのような背景を知ることで理解を深め，疑問を持ち，発展させることも可能になるのではないだろうか。
＜授業改善の工夫のポイント＞ 変形の背景を知り学習目標を把握する
加法定理を逆にたどれば２つの波を１つの波に合体（合成）できるはずだ。
（展開） 一通り合成の手順を説明・練習した後，ポイントを確認
「正弦の加法定理を逆にたどるので，2つの波は同じ周期の正弦波＋余弦波」
[生徒の様子]
- ・「余弦の加法定理は逆にたどれない？」
- ・「周期が異なる波は合成できない？ 周期が違う音だって和音になるはず。」
- ・「周期が同じ音，違う音ってどうなの？」
- ・「正弦波＋正弦波は？ あっ振幅を足せばいいだけか。でも周期が異なると？」
ex. y=sinx+cosax のグラフの変化 ・・・・・ function view を操作
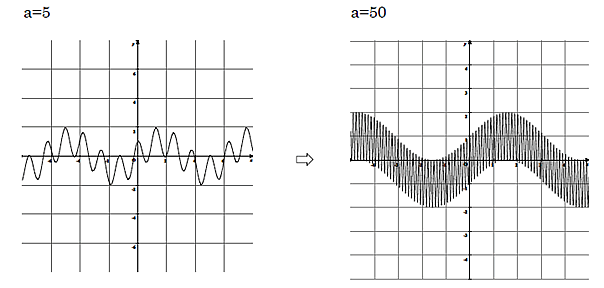
| ・ a=５のとき | 「確かに周期的な波みたいにはなってるけど複雑そー」 →音叉と楽器の音色についての話 |
| ・ a=50のとき | 「なんだか太い正弦曲線みたい」 「もっとaの値を大きくしてみよう」 → a=245 , 492 あたりでびっくりするような曲線になる |
ICTを利用した活動中，数学的説明はなるべく簡単にして深入りすることはしなかった。それよりも「とっつきにくいただの塊みたい」（生徒）だった三角関数の合成が，多少なりとも色鮮やかに見えたのであればそれでいい。生徒が自らの言葉で話し，考え始めるには大切な経験であったと感じる。
③ 提案「幾何」
高校の図形領域は，図形の性質（数学Ａ），図形と方程式（数学Ⅱ），ベクトル（数学Ｂ）複素数平面・いろいろな曲線（数学Ⅲ）で構成されている。特に「図形と方程式」「ベクトル」で学ぶ解析幾何やベクトル幾何の手法は高校幾何教育の中心に据えられ，「図形の性質」（初等幾何）を踏まえたうえでのより部分的・分析的な性質の考察ができるようにすることを目指している。同時に，これら図形に対する見方・アプローチの仕方は関連を持って学ぶことも重要である。
しかし，実際の授業ではたまに別解を示すことはあっても，それら相互の関連や種々のアプローチの方法を生徒自らが検討し考察を深められる機会はなかなかつくれない。それぞれの学習分野における閉じた発想・解法で完結し，与えられた問題の正解を目指すのみである。これは仕方のないことではあるが，指導する側としては本来この点において生徒たちの活発な学習活動を引き出す工夫を行い，まさに「練り上げること」で幾何教育の目的にすこしでも近づきたいところである。特に数学ⅡBまでを学び終えた３年生には一度はじっくり経験させたいところである。
＜授業計画案＞
下の例は有名なオイラー線を題材にし，ICTを利用した初等幾何的活動の中から注目すべき課題をとらえ，それを確かめるためにアプローチの仕方を比較検討させる授業を想定した計画案（メモ）である。
（導入）作図ツールGeometric Constructor（GC）を活用し，定義の確認と課題を把握する。
点Aをつまんで動かすことでそれに応じて点D，E，Fが動く。
「点D，E，Fは外心，重心，垂心のうちどれなのかを推測しよう」（定義）
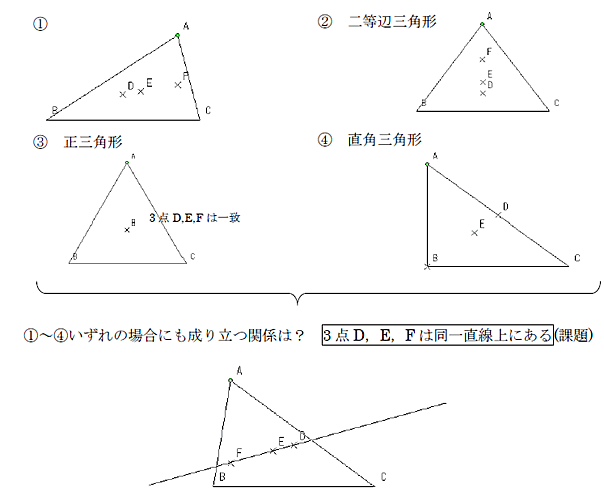
（展開）証明のアプローチ方法を検討する。
[初等幾何的] 直観やひらめきを求められる初等幾何的アプローチは難しい！
⇒ ３点の定義を確認させ，次の図を示す。
⇒ 定義，定理，性質などを用いて結論づける。
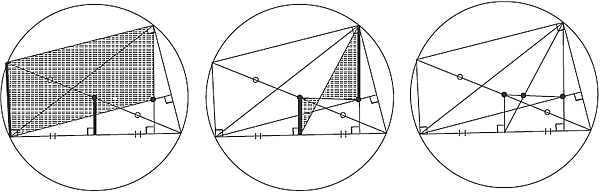
[解析幾何的] ①～④のどの図を用いて考える？（特殊化・一般化）
⇒ 座標軸をどこにとる？
⇒ ３点の座標から読み取れることは？
[ベクトル幾何的] キーワード「３点が同一直線上」をどう処理する？
⇒ まず点をベクトルとして扱う位置ベクトルについて（確認）
⇒ 始点をどこにとる？
⇒ 外心，重心，垂心の位置ベクトルを求める
⇒ どこを始点にとった場合がよかった？
以上の活動の後，次のような活動が考えられる。
⇒ それぞれのアプローチの優れている点，他と似ている点などについての考察
⇒ 内心や傍心についての検討
→ 「図形と方程式」「ベクトル」などの解析的なアプローチは困難
→ 定義が角度に依存しているため？
３．まとめと課題
今回取り上げたもの以外では，現在担当する数学Ⅲにおいて「あらゆる極限(値)は何かを意味する」をテーマに，得られた結果から何が分かるのかを，丹念に(ときには無理やり)吟味する活動を取り入れた。計算に興味を持たせられるだけでなく，関数値と極限値の微妙な違いに目を向けさせることにもつながった。こうして得られた理解は，学習内容を自分の力で深めるきっかけとなるものと期待している。
生徒自身が発展させたり深めたりする自発的思考活動を始めるには，まずはそのきっかけとなるような活動経験と，考える力を育む理解の仕方が必要である。そのための授業改善の方法は今後も継続して研究していきたい。
さらに評価の方法についても考えていく必要がある。指導と評価の一体という観点からも，自発的な学習内容の深化をねらった授業展開を考えるのであれば，それを評価する方法が必要である。