教師の方へ

授業実践記録（数学）

数学的論拠に基づいて判断する態度をはぐくむための指導方法について
－振り返りの場面で「他者を通して学ぶ」ことを通して－

広島県立広島高等学校　久冨　洋一郎

１．はじめに

高等学校学習指導要領解説（平成21年，文部科学省）に，数学科の目標は次のように掲げられている。

《数学的活動を通して，数学における基本的な概念や原理・法則の体系的な理解を深め，事象を数学的に考察し表現する能力を高め，創造性の基礎を培うとともに，数学のよさを認識し，それらを積極的に活用して数学的論拠に基づいて判断する態度を育てる》（ｐ.５）

この目標の末尾は「数学的論拠に基づいて判断する態度を育てる」とされているが，「数学的論拠に基づいて判断する」ことについては，《事象を数学的に表現し，正しい数学的推論によって得られた結果に基づいて合理的に判断すること》（ｐ.17）とある。そしてこのことこそが，高等学校における数学教育が現代社会を生きるために必要な資質・能力をはぐくむものとしている。

長尾（平成23年）はこれについて，次のように述べている。

《数学は，ある前提から正しい推論を積み上げて結果を得，それを体系的にまとめていく。したがって，この過程を繰り返し経験することによって自律性を育てることができると考えられる。大切なことは，一人一人の生徒が「正しい」と考える推論を積み上げることであり，根拠に基づききちんと結果を説明できるようにすることである》（ｐ.24）

数学科授業で言えば，例えば問題解決の場面において，その解決に至る過程では様々なアプローチがあり，その各場面で「正しい」数学的推論に基づく合理的な判断が求められる。教師には生徒がそのような数学的活動を積極的に行う場面を設け，目標にあるような態度をはぐくむ役割がある。各学校のカリキュラムはそうした目標を踏まえて作成されており，その目標を達成するために各科目における授業の具体化が図られなければならない。

平成26年度，筆者は第３学年理系の習熟度別の１クラスを担当している。主に第１学期に実施される数学Ⅲの履修以降は学校設定科目「応用数学」となり，これまでに学んだ数学的な内容や方法を基に，生徒の数学的な思考力や表現力を高めていく演習に移行する。生徒は事前に割り振られている課題について板書を行い，その解答を教師が確認していく形をとっている。対象クラスは，理系の生徒126名を習熟度別に５クラス編成した上位２番目の生徒32名である。数学的な知識や理解，技能の基本は備わっている生徒が多いものの，問題を取り組む際に分からない場合には解説を参考にし，その内容を理解し覚えていくという方法をとっている生徒も少なくない。このような学習方法では，定期考査等における類題については取り組むことができても，問題の表現が変えられたり，未知の問題に遭遇したりした際には対応できない場面も多く見受けられ，数学的論拠に基づいて判断する態度をはぐくめているとは言えない。

以上のことから，本実践では演習指導において生徒の多様な考えを引き出し，その考えを基に合理的な判断をさせていく学習場面を通し，生徒の数学的論拠に基づいて判断する態度をはぐくむための指導方法について考察していくこととした。

２．「他者を通して学ぶ」授業

第１学期期末考査後から数学の演習に入っていき，事前に担当する問題を割り振りしたものを生徒に板書させ，教師がその解答を確認するスタイルをとっている。多くの生徒は担当する問題について正答を準備し，その内容を板書し，教師がその解答について確認し，必要があれば説明の補足をしていく形になっていた。生徒は使用しているテキストの解説をもっていないが，テキストの巻末には略解とヒントがついており，それを参考にしている生徒も多いようであった。

平成26年７月の授業において，次のような問題を扱った。

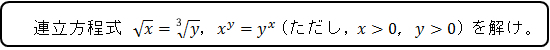
この問題を担当した生徒の解答の概要は次のようなものであった。

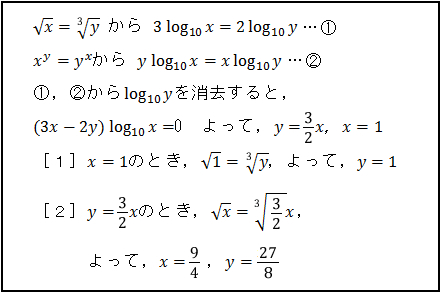
この解答は，テキストの略解にヒントとして提示されている方法と同じものであり，担当した生徒に確認したところ，略解を参考にしながら解答を作り上げたとのことだった。事前に筆者もこの問題を解いていて，担当した生徒の解答の確認をした後，筆者がこの問題を解いた感想について「は解にならないとは思わなかったか？（もちろん解にはならないのだが）」と聞いたところ，多くの生徒が「そう思った」という反応を返した。さらに，どのように処理をしようと思ったかを，筆者自身が考えた解法について説明したところ，ある生徒が「先生と少し違うのですが，この方法でどうしてうまくいかないのか分からない」と全体の前で次のような解法を提示した。

生徒は「この方法だとｘ＝１，ｙ＝１が出てこないことになり，何がまずいか分からない」と言ってくれ，「たぶん，指数を取り出すところが怪しい」と感想を述べた。生徒が予想した通りであり，命題「ａ ^ｐ＝ａ^ｑ → ｐ＝ｑ」の真偽を問うたところ，多くの生徒は気が付いたようであった。ａ＝１のときを考えれば偽になることが分かり，この点を注意すればから指数部分を比較する際に注意しなければならないことが分かる。この場面において多くの生徒は「なぜダメなのだろうか？」と考えていたように見受けられた。最初にこの問題を担当した生徒が示した解法は各式の常用対数をとって調べていく方法であるが，後に提示した生徒の解法の方がある種自然な思考の流れと考えられた。このような場面では多くの生徒が興味関心をもって意欲的に問題を考えようとしており，二宮（平成23年）が述べている「他者を通して学ぶ」ことにつながっていると言える。二宮は，教師は「他者から学ぶ」ことを数学の指導では留意すべきであり，さらに「他者を通して学ぶ」ことを推奨し，その違いについて，次のように述べている。

《「他者から学ぶ」という考え方には，他者が模範解答をもっていてそれを習得するという，従来的な学習観がその意識の根底にあるように思われる。正答を知っているか，知らないか，という非常に単純な二分法である。しかし，「他者を通して学ぶ」場合には，自分はすでに分かっているつもりである事柄についても，友だちの考えを知ることで，他者を通して更に何か学ぶべきものがあるはずであるとの信念のもと，積極的に相互作用（伝え合い）を進めていくことになる》（ｐ.103）

そして，そこから学ぶものは「内容的側面」のみならず，「方法的側面」かもしれないし，自分では気付かなかった新たな内容かもしれないし，他者の態度や信念などの情意的な事柄かもしれないと述べている。先に挙げた問題解決の場面はまさに上で述べたようなことに合致していると言える。このような場面が生徒の意欲を高め，数学的活動を活発にするきっかけになっていると感じられ，生徒の数学的論拠に基づいて判断する態度をはぐくむ可能性があると考えられた。

生徒は担当する問題についてクラスの生徒の前で板書するため，「間違えたくない」という意識が強く，周りの友人に聞いたりヒントを参考にしたりして正答に結びつけようとすることが多いと考える。しかし，このように正答ばかり出てしまうと，本来生徒がもっている多様な考えを授業の場面において十分に生かすことができない。先に述べたように，「他者を通して学ぶ」場面を積極的に設けていくためには，問題解決において正答誤答は関係なく様々なアプローチを扱っていくことが重要であると考え，以後の授業においては次のようにすることとした。

問題を予習する際，略解（ヒントも含む）を見ず，自分なりの考えをまとめ，発表すること。

数学の問題に取り組む上でこうした条件を設定することにより，生徒は略解やヒントを参考にせずに，自分なりの解答を考え，またそこで考えたことを自分のことばで説明し，他者と共有することにより，上述した態度の育成ができると考える。そのことが生徒にどう影響していくか，一定期間の実際の授業場面を振り返ることと，生徒へのアンケート調査の結果を分析していく。

３．授業実践

平成26年７月から10月までの約２か月間，前節で示した条件のもと，授業実践を行った。本期間で取り扱った題材は次の表１の単元の内容である。

表１：実施した科目名（単元）と問題数

科目	単元	問題数
数学Ⅱ	微分・積分の考え	14
数学Ｂ	平面上のベクトル	８
数学Ｂ	空間のベクトル	２
数学Ｂ	数列	10
数学Ⅲ	極座標と極方程式	２
数学Ⅲ	関数	４
数学Ⅲ	極限	12
数学Ⅲ	微分法	15

生徒は予習をした上で，発表の担当になっている問題については授業前までに板書し，自分の考えた方法を発表し，その後，その発表内容について教師とともに振り返るようにしている。授業実践期間における全授業時間数は29時間であり，１時間につき２～３題扱った。

この条件に基づき授業を進めた際，生徒が板書した内容を説明した後の振り返りの場面では，次の２点が特徴として現れた。１点目は32名の生徒のうち，約３分の１程度が「このような考えはダメなのだろうか？」と自分の考えを提示し，その内容について他の生徒と共有する場面をもったことである。そして，２点目は数学的な原理や概念，規則に対し，生徒が誤解をしていると考えられる場面があった際，教師がその内容について生徒に発問を投げかけたり，逆に生徒から疑問が出されたりしたことである。これらの２点について，具体的な場面を挙げ，分析していく。

●別解が挙げられた問題場面例

次の問題①の事例を分析していく。

問題①［数学Ｂ：数列］
　　次の３つの条件をすべて満たす三角形の３辺の長さを求めよ。
(Ａ)　最大角と最小角の差は90°である。
(Ｂ)　３辺の長さを大きさの順に並べたものは等差数列である。
(Ｃ)　３辺の長さの和は３である。

問題①を発表した生徒Ｓ１による解法は次の図１のものであった。

図１：問題①において生徒Ｓ１が板書した解答

生徒Ｓ１は条件 (Ｂ) から等差数列であるので，３辺の長さをｌ－ｄ，ｌ，ｌ＋ｄとおいて説明をしている。条件 (Ｃ) によりl＝１はすぐに分かり，その後は正弦定理や余弦定理を用いてｄを求めている。テキストの解答例においては，３辺の長さを短い方からａ，ｂ，ｃとおいて説明をしているが，立式した後の計算においては３辺の長さについて対称性を利用した生徒Ｓ１の解法の方が本問題においては有用であると考えられた。授業後に生徒Ｓ１にインタビューしたところ，「最初は解答例と同様に３辺の長さをａ，ｂ，ｃとおいて計算を進めていたが，途中に出てくる４次方程式がどうしても解けなかったので，別のアプローチを考えた」とのことだった。このことから問題①に取り組む上で様々な解法を考えようとしている姿勢がうかがえた。

そして，問題①を振り返る場面では，生徒Ｓ２から「図形（図２）を使って処理してはダメなのだろうか？」という質問が出てきたので，生徒Ｓ２の考えを全体で共有することとした。

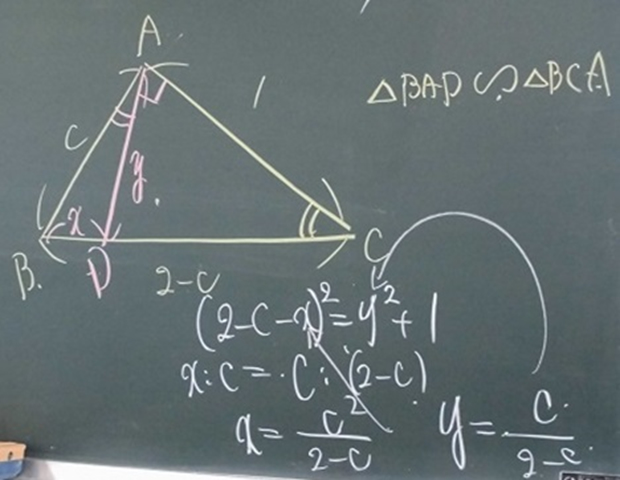
図２：生徒Ｓ２が発表した内容を教師が板書したもの

図２の内容については，次のようになる。

３辺の長さを長い方からａ，ｂ，ｃとおき，条件 (Ｂ) と (Ｃ) からｂ＝１，ａ＝２－ｃとなる。このとき，条件 (Ａ) から∠Ａが鈍角になることが言えるので，∠CAD＝90°になるように点Ｄを辺BC上にとることができる。このとき，△BADと△BCAが相似になるので，BD＝ｘ，AD＝ｙとおけば，対応する辺の比が等しくなることと，三平方の定理を使うことで求めることができる。

生徒Ｓ２は生徒Ｓ１が発表したような方法は思いつかず下線部分にあるよう，補助線を活用し幾何的に解くことを試みたところ，このような方法を思いついたとのことだった。この別解については多くの生徒が意外なほどにシンプルにできることに驚いていた。図形問題では，三角比やベクトル，座標（解析）幾何によるアプローチが高等学校では主となるが，初等幾何の良さを感じられる場面となった。

●生徒が数学の概念を誤解していた場面例

次の問題②の事例を分析していく。

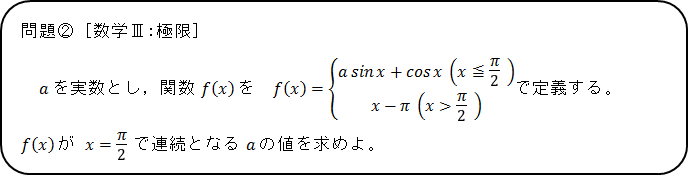
問題②を発表した生徒Ｓ３による解法は次の図３のものであった。

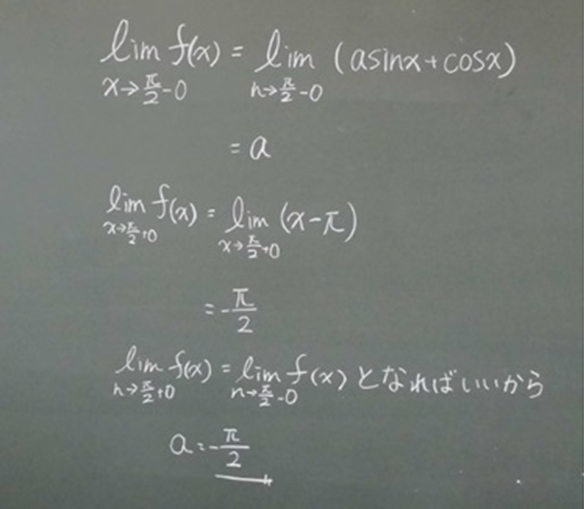
図３：問題②において生徒Ｓ３が板書した解答

この解答例は関数が連続であることの条件を誤解しているものである。しかし，実際には図３にあるが答えとしては正しいものとなっている。すなわちで連続となるための必要条件の一つであるの存在だけから，ａの値が実際に出てくることでそれを解答にしている。この場面では教師から全体に向けて「ａの値は出てきているけど，これでいいのかな？」と発問を行ったところ，生徒はとなることを言わなければならないと発表したので，教師から「どうして，そうならなければならないのだろう？」と連続の定義を振り返る場面をもった。その際，となる関数の例を挙げ，関数の連続の定義について理解を深める場面をもった。実際，生徒Ｓ３と同じような誤解をしていた生徒は，その場面があったことにより連続の定義について再認識していた。なお，平成26年10月に実施した定期考査において，関数の連続性について，次の問題を出題したところ，生徒Ｓ３の解答は図４のようになっており，関数の連続性についての理解が深まっているととらえられた。

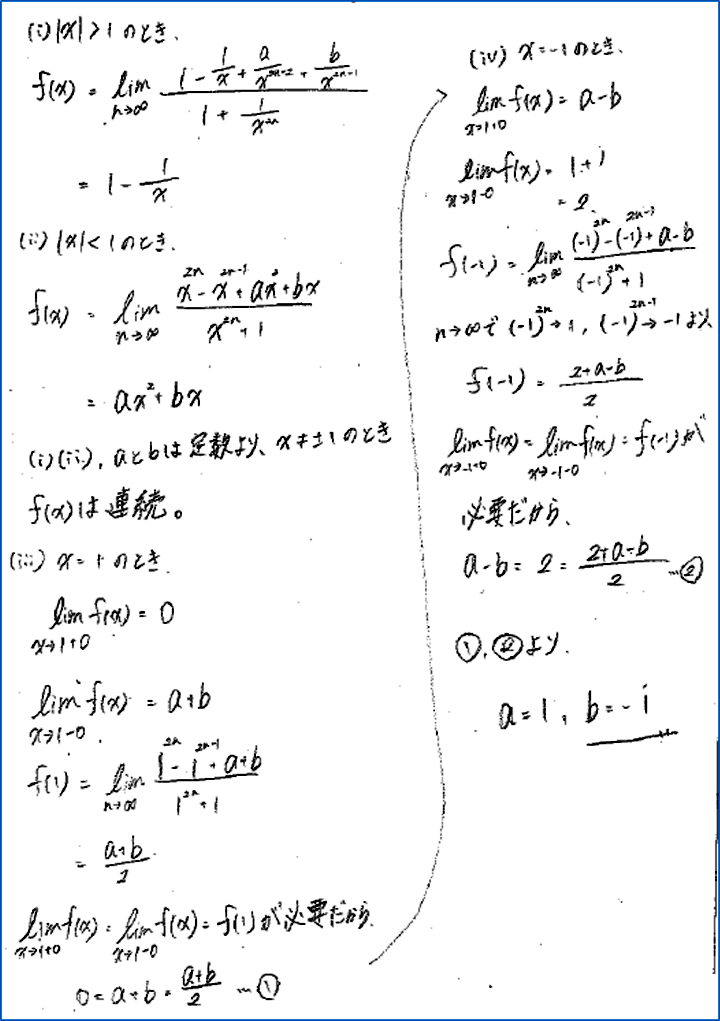
図４：定期考査における生徒Ｓ３の解答

●授業アンケート分析

平成26年10月の授業時に約２か月間の授業についてのアンケート調査を実施した。次の質問項目に対する生徒の回答状況を挙げておく。

（１）略解やヒントを見ずに問題に取り組んで，計画的に予習を行いましたか。

類型	人数
ア：まったくヒントなしに取り組んだ	14人
イ：時々略解におけるヒントを見て取り組んだ	５人
ウ：時々友達に教えてもらい取り組んだ	３人
エ：その他	10人

「その他」を選んだ生徒の中には「予習自体をあまり行わなかった」と答えた生徒が２名，他の問題集などを参考にして考えたという生徒が２名などであった。多くの生徒が与えた条件のもとで問題に取り組んだことがうかがえた。

（２）大問１問の問題に取り組む上でおおよそ何分考えましたか。

類型　※未回答：１名	人数
ア：10分未満	１人
イ：10分程度	５人
ウ：20分程度	13人
エ：30分程度	７人
オ：30分以上	５人

問題に取り組む時間は20分から30分程度が多いことが分かった。

（３）自分のこれまでの数学の問題に取り組む姿勢と今の姿勢に変化はありましたか。

類型	人数
ア：変化があった	23人
イ：特に変わらない	９人

「変化があった」と回答した生徒には，どのような変化があったか，自由に記述してもらったところ，次のような内容が挙がった。

○昔は解いていて行き詰まると10分もしないうちに諦めていたが，今は20分以上考え続けることが普通になった。加えて，以前は考えているつもりで思考停止している時間が長かったが，今は様々な別のやり方への手口がないかひとつひとつ当たっていくことができているような気がする。

このように，問題に取り組む際に粘り強く考えるようになったという生徒が他にも９名いた。

○以前は解答さえ合っていれば後は何とかなるかなと考えていたが，日本語での説明も意識して書くようになった。

自分が発表したり，他の生徒が発表した内容を聞いたりすることにより，相手を納得させるための説明の仕方などに対して意識を払うようになったと答えた生徒が他にも３名いた。

（４）その他，このような授業スタイルについての感想（良かった点，悪かった点などを具体的に）や要望など，自由に記述をしてください。
次のような回答が多く挙げられた。

○思いもしない解き方をしている人が多くいてすごいなと思った。

○当たった問題を前でしゃべるのが難しかった。黒板にどれぐらい書けばいいのかもよくわからなかった。みんな上手に説明していてすごいと思った。でも解説を自分ですると理解は深まると思う。

○答えを見ずにある程度考えていたら自力でできるような問題も意外にあったのでよかったと思います。

教師ではなく自分が説明したり，他の生徒の発表を聞いたりすることにより内容の理解が深まり，問題の解決に向けての興味や関心が高まり，ひいてはそのことが数学学習に対する意欲を高めるとこにつながる生徒が多いことがうかがえた。

４．まとめと考察

以上のように「問題を予習する際，略解（ヒントも含む）を見ず，自分なりの考えをまとめ，発表すること」という条件のもと，学習指導を行い，授業ならびにアンケート結果を分析した結果，次の２点が明らかになった。

（１）生徒が問題について様々な角度から粘り強く考えるようになり，生徒の数学的論拠に基づき判断する態度をはぐくむ傾向がある。
（２）授業において生徒が考えた解答を発表したり，他の生徒の発表を聞いたりすることにより，自分の考えを振り返るなどの反省的思考を促している。

結果（１）については，アンケート調査の分析により，多くの生徒がこれまでよりも数学の問題に粘り強く取り組むようになったと答えている。また，略解などのヒントなしで取り組むことにより，問題解決に向けて多様なアプローチを行い，自分の考えについて筋道が通っているかどうかという「正しい」数学的な推論に基づく合理的な判断を各場面で行っている。これらのことを継続的に行うことで，自分の考えに自信を持つことができている生徒も増えていることが分かり，生徒の数学的論拠に基づき判断する態度の育成につながっていると言える。

結果（２）については，考えた解答を全体の場面で説明することにより，相手に理解してもらうと同時に自分の考えたことを振り返っていることが分かる。また，他の生徒の考えなどを聞くことで，自分の考えと比べ，発表した生徒だけでなく，全体の生徒の反省的な思考を促すものとなっている。このことは「他者を通して学ぶ」ことができていると考えられる。とりわけ，数学的な概念や規則についての誤解について共有した際には，その内容について理解を深められる場面をもつことができている。板書する内容が正しい記述ばかりであっては，このような誤解を生かす場面を設けることは難しいと考える。

これらの結果から，教師の授業における役割は，生徒の数学的活動を促すような学習場面をどのように設けるかということであると考える。生徒の考えを中心にした演習授業の構成を行うことにより，「他者を通して学ぶ」ことができ，生徒の数学に対する関心や意欲も高まっていると考える。しかしながら，このような授業のスタイルは数学に関する一定の知識や理解，技能を有している生徒だからこそ可能であるとも考えられる。今後の課題は，他の習熟度の生徒にとってもこの方法が有用なものとなるのか，継続した実践を行うことにより検証をしていくことである。