
授業実践記録(数学)
数学Ⅰ・数学Aにおける課題学習の取組について
1.はじめに
平成24年度から実施されている教育課程では,数学Ⅰ・数学Aにおいて課題学習が導入された。学習指導要領では「数学Ⅰ・数学Aの各単元の内容又はそれらを相互に関連付けた内容を生活と関連付けたり発展させたりするなどして,生徒の関心や意欲を高める課題を設け,生徒の主体的な学習を促し,数学のよさを認識できるようにする。」とあるが,適切なテーマを設定するのは難しい。私自身も昨年度新課程の1年生を初めて受けもち,課題学習の扱いに試行錯誤した。ここでは,昨年度私が実践した課題学習の取組を紹介する。
2.実践例①「身近な2次関数~自由落下運動~」
2次関数が身近に表れている例として,物体の落下運動がある。そこで物理の先生にも協力していただき,記録タイマーを用いて落下運動に関する実験を行った。
○授業の展開
(a) 事前指導
対象生徒は文系の生徒であり,物理を履修しない。そこで,この実験の前に等加速度運動や重力加速度について簡単な講義を行った。その中でV-tグラフの傾きが重力加速度になることも説明した。
(b) 実験
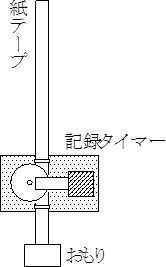
- (1) 図のように,記録タイマーの台板の面を鉛直にしてスタンドに固定する。
- (2) 約1mに切った紙テープを記録タイマーに通し,上端を手で支えて,下端におもりをクリップでとめ鉛直につるす。
- (3) おもりが落ちる位置にクッションを置き,記録タイマーをはたらかせてから手を放しおもりを落とす。
(c) データ処理
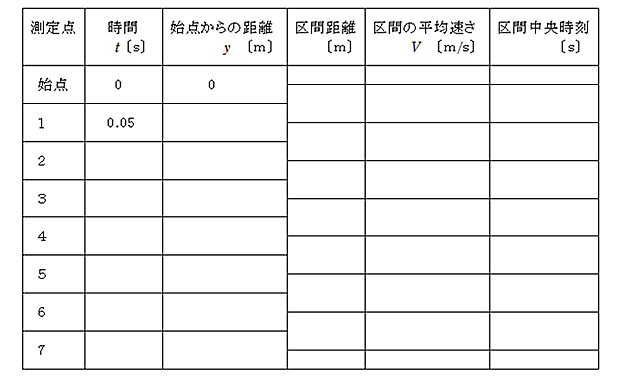
- (1) 紙テープの点とわかる最初の打点を始点とし,始点より3打点毎に測定点を取り区間を定める。

- (2) 始点より各測定点までの距離(y)をものさしを用いて測り,表に記入する。
- (3) 表をもとにして,y-tグラフを描く。
※ タイマーの打点間隔は,関西での交流の周波数が60Hzであることから1/60〔s〕となっている。したがって,1区間の時間は1/60×3=0.050〔s〕である。 - (4) 区間距離を計算し表に記入する。
- (5) 各区間の平均の速さ(V)を求め、表に記入する。
※ 区間の速さは 区間距離÷0.050 で求まる。各区間の中央の時刻を結果の表に記入する。 - (6) 表をもとにして,V-tグラフを描き,傾きを求める。このとき,『各区間の平均の速さはその区間の中央の時刻の瞬間の速さに等しい。』ことを用いる。
※測定結果記録表
(d) 考察等
- (1) V-tグラフの傾きから重力加速度〔m/s2〕を求める。
- (2) 実験から得られた重力加速度と実際の重力加速度との誤差の割合
(測定値-9.80)×100/9.80〔%〕を求める。 - (3) 誤差の原因として考えられることは何か,またその他疑問に感じたことや感想などをグループで話し合う。
(e) 事後指導
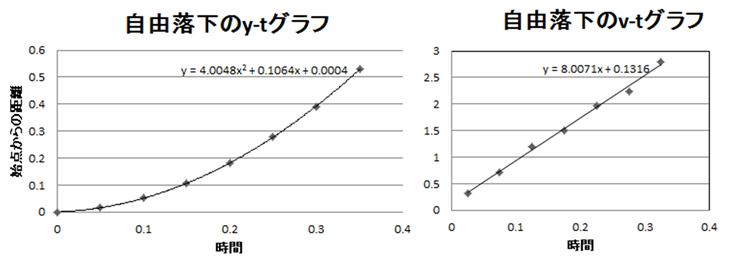
今回の実験ではy-tグラフやV-tグラフをグラフ用紙に描いたが,このデータを「データの分析」の授業の実習にも用いた。コンピュータで表をつくり,近似曲線を用いてグラフを描き自分で描いたグラフと比較させた。下のグラフはある生徒がコンピュータで描いたグラフである。
○生徒の感想
- 物の落下と2次関数が関連していることに驚いた。
- 重力加速度の値が実際の値とかなり違っていたが,まっすぐおもりを落とせていなかったことに原因があるのかもしれない。
- また,このような実験をやってみたい。
3.実践例②「オイラーの多面体定理を確認してみよう」

正多面体などの空間図形は生徒にとってイメージすることが難しい。そこで折り紙を用いて実際に正多面体を作製し,オイラーの多面体定理を確認することとした。合わせて半正多面体についても紹介したうえで展開図から半正多面体を作製し,オイラーの多面体定理を確認させた。写真は生徒が作製した多面体・半正多面体である。
なお,この授業はシンガポールの高校が学校交流で本校を訪れた際の合同授業として他のクラスでも行った。残念ながらこちらが英語で授業をするということまではできなかったが,生徒は積極的に英語を用いて多面体の作り方を教えており,良い交流ができたと思う。また,シンガポールの生徒にとっても授業で扱われていない「オイラーの多面体定理」を知るとともに,日本の文化の一つである折り紙を体験でき有意義だったのではないだろうか。
○生徒の感想
- 多面体というものは文で見るだけではなかなかイメージできなかったが,実際に見てよく分かった。
- 普段はこのような作業をすることがないので新鮮で楽しかった。
- どんな角・辺をもつ多面体になろうとv-e+f=2というのは不変であることに非常に驚いた。
- これからは,問題を解いていく中で計算の方法などを考えていきたい。
4.おわりに
今回紹介したものの他に,「正五角形と黄金比」…正五角形の対角線の長さや72°の正弦・余弦の計算,黄金比や白銀比・フィボナッチ数列についての紹介,「暗号を作ろう」…整数の性質を用いたRSA暗号による簡単な暗号の作成・解読,「必勝法を見つけよう」…整数の性質を用いてゲームの必勝法を探る,といったテーマで課題学習を行った。文系の生徒が対象であり数学を苦手とする生徒も多いのだが,グループで協力し合い楽しんで活動する姿が印象的であった。少しは数学の面白さを感じてくれたのではないかと思う。今後も生徒の関心意欲を高められるような授業を目指して努力していきたい。
参考 『数学活用』(啓林館)
「アルキメデスの立体 紙模型のコーナー http://www7b.biglobe.ne.jp/~geomzome/archimedian_solid.html」


