数学Ⅱの平行移動を含む三角不等式解法についてのひと工夫

１．はじめに

数学Ⅱの三角関数において，X軸方向の平行移動を含む三角方程式・不等式の解法を指導する方法は，単位円またはグラフを利用するのが，一般的である。しかし，これだけでは理解できない生徒が多く，視覚的にとらえ納得できる指導方法のひとつとして実践し生徒の反応がよかったので紹介したいと思う。

２．ねらい

度数法から弧度法への移行は，生徒の理解が不十分なうちに，基本の三角方程式・不等式へと進んでさらに合成により，X軸方向の平行移動を含む三角方程式・不等式の解法が必要となる。そこで，単位円を数直線の帯へと移すことを利用し基本で求めた数値および範囲がどこに移動しているかを視覚的に理解できるようにする。

３．授業展開

基本形である sinθ， cosθ， tanθ （０ ≤ θ < ２π） の方程式・不等式を十分に指導した後に平行移動を含む等式・不等式を単位円のみで出来るように指導する。この指導後に演習をしてみると出来ない生徒が多いので，そこでこの数直線の帯による指導をすることでこの利便性が理解できるようにする。

４．指導内容

【例題】０ ≤ θ < ２π のとき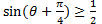，を満たすθの値の範囲を求めよ。

（解答）

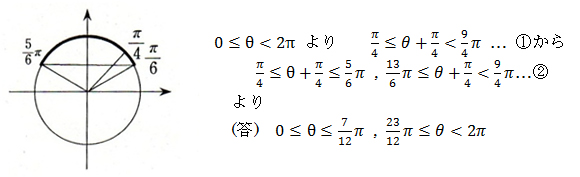
であるが，単位円で，①から②を導く過程で数学の得意でない生徒は基本の答えである 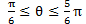との関係が理解できない。そこで，単位円の部分を数直線の帯を使い，基本の答えである 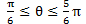との関係がどのようになっているかを理解させ②の解を導く方法を指導する。

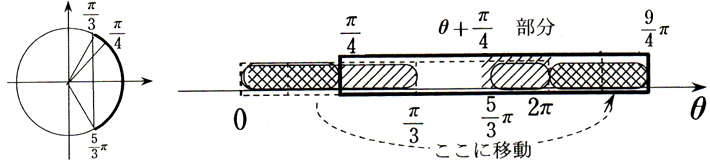
＜数直線の帯＞

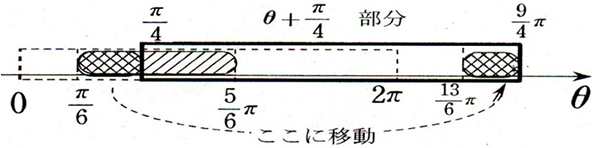
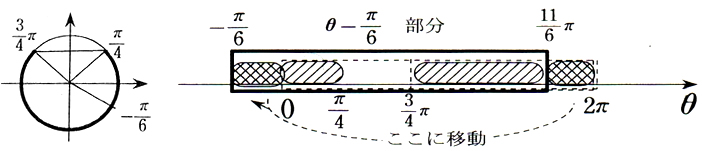
点線の帯が ０ ≤ θ < ２π で，その中で解いた解の一部 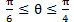が太枠の帯の外にあり，その部分が右端の 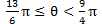に移動することを説明することで，解答の②の後半部分が単位円よりも大小関係が視覚的に理解できる。

＜参考１＞　右端に移動する問題

【例題】０ ≤ θ < ２π のとき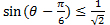， を満たすθの値の範囲を求めよ。

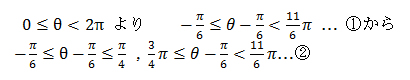
＜参考＞　余弦の場合について

【例題】０ ≤ θ < ２π のとき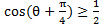， を満たすθの値の範囲を求めよ。

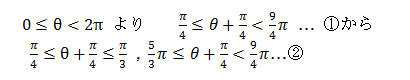
５．生徒の様子

実際の授業では，色チョークを使用し，はみ出した部分の移動がさらに視覚的に理解できるので，楽しく図を書きなが取り組んでいる。慣れてくると，だんだんこの数直線の帯を使用しないで出来るようになる生徒もいて，効果を感じた。

６．おわりに

数直線の帯でなく，数直線のみで出来るのであるが，範囲を考えるときに数直線だけだと，図がわかりにくくなるので帯を利用する方が効果は大きい。また，理解でき練習を積むことによって単位円のみで出来るようになるので，その一過程として利用していけば良いのではないかと感じている。また，今後更に研鑽を積み，他の分野でも，視覚的に出来る分野への工夫を考えていきたい。拙稿をお読み頂き，ご教示下されば幸いである。