
授業実践記録(数学)
「第1学年 空間図形 立方体の切り口の形を考えよう」
-発問を核として数学的表現力を高める授業づくりを目指す-

1.はじめに
平成20年の学習指導要領改訂に伴い,学力の3要素の1つとして思考力・判断力・表現力が挙げられ,数学の目標にも「表現する力」という文言が改めて明記された1)。数学的表現力は従来,表現・処理という観点に含まれていたが,今回,思考力・判断力とともに言語活動を通して培われる力として明示されたものである。
一方,普段の授業を振り返ってみると,計算手順等の手続きに関する学習には熱心なのだが,その背後にある意味や論理にはあまり興味を示さず,「なぜそうなるのか」ということを聞くと,うまく説明ができなかったり,あまり関心がなかったりする生徒たちが多い。数学の学習は,計算のやり方に代表される手続きの理解が不可欠なだけに,その習得に重きをおかれがちである。その結果,授業は「手順の説明―適応練習」の形式に陥りがちである。
そこで,「なぜ?」「どうして?」という気持ちで課題に向かい,説明したり,根拠を明らかにしたり,伝え合ったりする活動の場を授業の中に設定することで,生徒の数学的表現力*が高まり,その結果,より深い数学の理解が得られるのではないかと考えた。
*本稿で用いる数学的表現力とは,①言葉や数,式,図,表,グラフ等さまざまな表現方法を用いて事象を数学的にとらえ,それを解釈する力 ②得られた理解を友達に伝えたり,友達の理解に触れたりして自分の考えを振り返り,理解を深める力 を指すものとする。
2.発問について
1 なぜ発問か
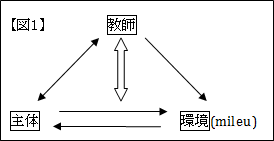
発問に着目した背景には,フランス数学教授学*がある。生徒は,「教師が正しいことを教えてくれる」という受け身の姿勢で教師のもっている答えを探す作業を行うのではなく,生徒自身が環境(ミルー)との相互作用で知識を構成していくという考え方である(図1参照)。
そのため,教師が生徒に問題を与えるのではなく,生徒自身が問題意識をもつこと,そしてその問題に対する考えを検証する場が与えられていることが重要になる。授業の中で生徒は,既習事項をもとに議論を進めながら,新しい発見を行い,知識を深めていくのである。時には誤った考えに陥ることもあるかもしれないが,教室の中の練り上げにおける友達のやりとりの中で考えの妥当性を検証する機会を与えられ,誤っていればそこで修正していくわけである。
その雰囲気を作り,授業の流れを作っていくのが教師の発問である。授業の中で培われた数学の問題に対する生徒の姿勢は,自らの考えを振り返り,気づき,発展させる原動力となる。数学的表現力を高めるために行われた発問は,やがて生徒が数学に向き合う時に自分自身に問いかける言葉となっていくことが期待される。そのため本稿では,発問という視点から,数学的表現力を高める授業について考え,授業改善を図っていく。
*1960年代に,ピアジェの均衡化理論を基盤として考えられ,Brousseauらによって確立された学問である。
2 数学的表現力を高める発問
数学的表現力は,他者とやりとりをする中で高められていく。そのやりとりを活性化するもととして,Balacheffは「問題提示の工夫」と,「反例の提供」を提案している。ここではその考えを参考に,数学的表現力を高めることができる発問の流れを提案したい。生徒が授業の課題を決定し,その解決の方針をたて,練り上げを通して解決していく流れを発問の視点からとらえ直すことで,数学的表現力を高めることができないだろうかということである。
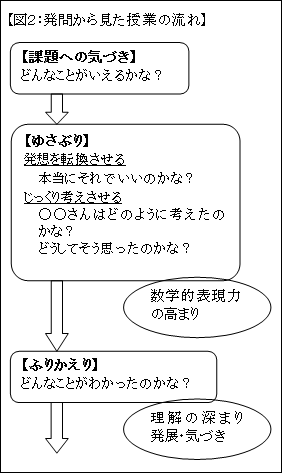
まず,授業は問題解決の形で行われることが望ましいのはいうまでもない。そうすると,一般的に授業の流れは,生徒の活動から見ると,「問題把握→自力解決→比較検討→振り返り→練習問題」というスタイルになる*。一方,教師側の発問の視点から見ると,大きく3つに分けられる。「課題への気づきの発問→ゆさぶりの発問→振り返りの発問」であり,下記の図のようになる(図2参照)。
*ポリアはその著「いかにして問題を解くか」2)で,①問題を理解すること ②計画を立てること ③計画を実行すること ④振り返ってみること の4段階を提示している。一般的に算数数学の学習指導案は,この形に添って学校毎に独自の形式で作られている。
(1) 課題への気づき
問題設定に関わる発問である。生徒が自分で問題を設定できるような場作りを行う。例えば,文字式の証明の単元であれば,数や図形に潜む不思議さに着目させ,生徒が発見したことをもとにその日の課題を決定する流れが考えられる。
発問例:「どんなことがいえるかな?」 「いつでもいえるかな?」 など
(2) ゆさぶり
生徒は,問題を考える過程で,自分の考えと友達の考えを比較したり,友達の考えを聞いたりして自分の考えを振り返ることになる。したがって,発想を促したり,発想を転換させたりする発問が必要になる。ここでは2つの発問のパターンを提案したい。1つめは発想を転換させる発問,2つめはじっくりと考えさせるための発問である。
ア) 発想を転換させる発問
自分の考えでは矛盾が出てきてしまったり,納得できないもやもや感が生まれたりすると,そこから議論が始まる。
発問例:「本当にそれでいいのかな?」
「どんな方法ならうまく説明できるかな?」
「いつでもいえるかな?」 など
イ) じっくり考えさせる発問
図に表したものを言葉で読みかえる,式で表したものを言葉におきかえて読む,表からいえることを言葉で説明する等,言語を通して数学と授業をつなぐ活動になる。ここでは,友達の意見や考えをその人の立場になって汲み取ったり,再構成したりする発問が望ましい。
発問例:「○○さんはどう考えたのかな?」
「○○さんの代わりに説明すると?」
「図からよみとれることは?」 など
また,なぜそう考えたのか聞くと,「ただなんとなくそう思いました」「ふつうにやった」と生徒は説明することが多い。なぜそう思ったのか,根拠を必ず問うことで,考える場が生まれるので,自力解決の際に自分の考えの根拠を明確にすることが大切だと常々から伝え,必要に応じて随時問うことで考えを深めていきたい。
発問例:「どうしてそう思ったのかな?」
「どんないいことがあるのかな?」 など
(3) ふりかえり
比較検討後に振り返る場面での発問である。ここでは単に授業でやったことを振り返ってまとめるだけでなく,さらに数学的に1段階深まった知識に気付いたり,気付かされたりする場になることが期待される。生徒の言葉で教室全体が気付きに持っていければよいが,生徒側からなければ,教師側から投げかけて知識の深まりを全体で共有したい。
発問例:「(○○さんの考えから,)さらにどんなことがいえるかな?」
3 学びの系統性
つくば市では,市内すべての小中学校がそれぞれの中学校区で小中一貫教育を行っている。竹園東中学校も,竹園東小学校,竹園西小学校と共に,「竹園学園」という施設分離型小中一貫校として活動している。単なるイベント交流ではない一貫教育を目指し,平成25年度には9カ年の連続した「学びのスキル系統表」を作成した。算数・数学科では全国学力・学習状況調査の分析をもとに,①既習事項をもとに,考えを伝え合い,深め合う力 ②数学的表現方法を活用する力 の2つの力に焦点をあてて育成を図っている。
資料1参照
さらに平成26年度は,このスキル表をもとに授業実践を行うほか,数学的表現力を高めるために大切にしたい言葉についてまとめなおし,児童生徒に配付して授業の中で意識して使えるように,児童生徒用スキル表を作成した。平成27年度には,全児童生徒にスキル表を配付し,教科書に貼って適宜活用している。
資料2参照
3.授業実践
1 指導案
7年1組 数学科 空間の図形
■ つくば竹園学園小中一貫教育の授業づくり
| 【本学園の課題】 | 1 既習事項をもとに,考えを伝え合い,深め合う力 |
| 2 数学的表現方法を活用する力 |
【本単元における課題克服の手立て】 空間図形の理解では,既習の図形に関する知識をもとに想像して立体について考える場面が必要になる。練り合いの時間を設け,友達の考えを聞くこと,なぜそうなるのかを考えることを通して理解の深まりを狙う。
■ 学びのスキルの系統性
| 既習のスキル | 本単元で身に付けるスキル | 今後身に付けていくスキル |
| 1 ⑥根拠を用いて考えを説明することができる。 2 ⑤図形の性質を操作活動を用いて説明することができる。 |
1 ⑩他者の意見と関連づけて考え,発表することができる。 2 ⑩見通しをもち,既習事項から類推し,問題解決を図ることができる。 |
1 ⑪数や図形について見いだしたことが一般的に成り立つか検討することができる。 2 ⑫帰納的考えで事象を読み演繹的に証明することができる。 |
■ 本時の学習
(1)目標
小学校で学んだ図形の知識と中学校で学習した空間図形の知識を組み合わせ,見取り図では表現しにくい切断面の形を想像したり,伝え合ったりできる。
(2)展開
| 学習計画及び学習内容 | 指導上の留意点 ◎評価 ★「学びのスキル系統表」を踏まえた手立て ☆発問 |
| 1 円錐を切断した時にできる形について考える 2 本時の課題を知る 立方体を1つの平面で切断してみよう。 切り口の形はどのような形になるだろうか。 また,なぜそうなるのか考え,説明しよう。 3 見取り図に切り口の形をかき入れて,なぜその形になるのか理由を考える。(グループによる活動) ・お互いの考えを話し合い,模型を使って正しいかどうか検討する。 4 考えを発表する ・作った図を黒板に貼って説明する。 【予想される生徒の反応】 ・三角形(正三角形,二等辺三角形など) ・四角形(台形,長方形,正方形,菱形など) ・五角形 ・六角形 ・七角形や八角形はできないのか考える。 5 わかったことをまとめる ・立方体の切断面の種類はいくつかあり,それは立方体の面や辺の長さや角度,平行や垂直の関係に着目することで説明できる。 ・七角形以上はできない。 |
・円錐曲線について簡単に紹介する。深入りはしない。 ☆どんなことがいえるかな?(課題への気づき) ・考えたこと,思ったことを周囲の友達と話すことで表現しやすい雰囲気づくりに努める。 ・例を挙げて等しい長さ,角度,平行,垂直に着目することに気づかせたい。(場づくり) ☆なぜそういえるのかな? ・解決はグループだが,見取り図は1人1枚完成するように指示する。 ・班に1つ模型を用意する。 ★習ったことをもとに理由を考えるように伝える。 ☆なぜそういえるのかな? ☆本当にそれでよいのかな?(ゆさぶり) ◎A:図形の性質に着目して,さまざまな断面図の形を説明できる。七角形以上ができない理由についても説明できる。(ワークシート・発表・話し合い) B:自分の考えた断面図の形について図形の性質を使って説明できる。 ☆ということは,どういうことなのかな?(ふりかえり) ・既習の図形の性質を使って新たな図形を見ていく大切さに気づかせたい。 |
2 授業の様子
(1)円錐の切断
断面の形については,二等辺三角形,円,楕円などいろいろな考えがでてきた。円錐の切断面の模型を見ながら,全体で確認した。確認後「どんなことがいえるのかな?」と聞き,「切り方によってさまざまな形が出てくる」という言葉から,本時の課題を導入した。
【本時の課題】
立方体を1つの平面で切断してみよう。どのような形になるだろうか?
(2)課題の説明(場作り)
「正方形になる」というつぶやきを拾って「なぜそのような形になるのかな?」と,聞いたところ,「4つの辺が同じ長さ」という答えが返ってきた。「同じ長さだと正方形になるの?」と返すと,直角というつぶやきはでてくるものの,なぜ直角になるのか答えられない。「今まで習ったことを使って考えてね。」というと,底面と側面が垂直になっていることに着目できた。
(3)課題の解決(グループによる解決)
1人1枚ずつ見取り図を配り,切断面を描き入れるように指示した。図には,そう考えた根拠を言葉や記号で書き入れるように指示した。
次にグループになり,自分の考えた切り口の形を友達に伝え,そうなる理由についてグループで話し合うように指示した。考えたり説明したりする時の材料として,グループごとに1つずつ立方体にゴムをかけた模型を用意した。

(4)発表(比較・検討)
なぜその形になったのか,全員のかいた図を形ごとに黒板に貼っていき,その理由について説明していった。模型を用意したことで,考えたり伝えたりしやすくなったようだ。
生徒たちは,等しい長さ,等しい角度,平行,垂直などに着目して三角形(正三角形,二等辺三角形)・四角形(台形,長方形,正方形,ひし形)・五角形・六角形に分類していった。

(5)ゆさぶり

「六角形までで全部なの?七角形や八角形はできないの?」と問うと,わからないと困った様子だったので,再度グループにして短い時間で話し合った。6つの面をゴムが全部通っているので六角形になること。立方体の面は6面しかないので七角形や八角形にはならないことが生徒の考えからでてきた。
(6)まとめとふりかえり

ワークシートに振り返り(今日の授業で何を学んだか)を書き,何人かの生徒に発表してもらった。「平行や垂直を探すと説明ができた。」「六角形までしかできないことがわかった。」などの発表があった後,ある生徒が「二十面体なら二十角形ができるのかな?」とつぶやいた。その生徒の考えを皆に話してもらい,一般化についての検討(いつでもいえるのかな?)もできた。
4.成果と課題
1 実践から得られたこと
生徒の数学的表現力を高めるためには,知識を伝える形式の授業から,教室の中で知識を生み出していく授業へと変える必要がある。そのために,本稿ではフランス数学教授学の考え方を参考に教師の発問に着目した。「課題への気づき→ゆさぶり→ふりかえり」という3段階の発問を重ねることで,生徒の数学的表現力が高まり,より深い理解が得られるという授業の枠組みを作ることができた。発問を重ねることで,生徒が自分自身に問い,発展的に数学を学んでいくようになることが期待される。
2 今後の課題
授業の中で,生徒が自分自身で問いながら考えを進めていき,数学の理解を得ている姿を増やしていくことがこの実践のねらいである。今後は,関数や文字式など他の分野でも発問を核として授業づくりをすすめ,よい教材やよい問いを作っていきたいと考える。そしてさらに,よい教材やよい問いが竹園学園の学びとして共有され,9年間を通した学びへとつながっていくことを願う。
【引用文献】
1) 文部科学省 学習指導要領解説 数学編 教育出版株式会社 2008.9
2) G.ポリア 「いかにして問題を解くか」 丸善出版株式会社 1954
【参考文献】
・文部科学省 言語活動の充実に関する指導事例集~思考力,判断力,表現力等の育成に向けて~【小学校版】2011.10
・根本 博 「数学教育の挑戦」東洋館出版社 2004
・N. Balacheff 「数学的証明の学習の改善(Improving Proof Learning)」 日本数学教育学会誌数学教育学論究 Vol.67・68,pp.52-62,日本数学教育学会 1997
・N. Balacheff "Towards a Problematique for Research on Mathematics Teaching" Journal for Research in Mathematics Education Vol21, 1990
・宮川 健 「フランスを起源とする数学教授学の『学』としての性格」日本数学教育学会誌数学教育学論究 Vol.94,2011
・原田耕平 「学校数学における子どものmisconceptionの同定と克服-Balacheffの教授理論を手がかりとして-」日本数学教育会数学教育論究vol.55,1991
・礒田正美・原田耕平 「生徒の考えを活かす問題解決授業の創造」 明治図書 1999
・田中博史 「算数的表現力を育てる授業」 東洋館出版社 2001
・水谷尚人 「中学校数学科 授業を変える「発問」と「課題提示」の工夫71」 明治図書 2008
・田中真樹子 「中学生文字式の論証に関するコンセプションの研究―見通しをもった意図的な式変形に着目して-」筑波大学大学院修士論文 2005


