| 授業実践記録 | |
| 曲線と接線と面積 |
|
| 駒澤大学高等学校 濱田敏明 |
|
|
1.はじめに
|
|
| 積分の単元では,放物線と直線や,放物線と放物線が囲む図形の面積の公式として,1/6公式はどの教科書にも問題集にも載っています。積分計算ができた上で,確認のための使用はとても有効です。これに関連して,放物線などの性質をちょっと話してあげることにしています。 |
|
|
2.展開
|
|
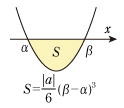
| (1)放物線と直線 [1] 2次方程式 ax2+bx +c =0 の2解がα,β(以下簡単のためα<βとします)であるとき,
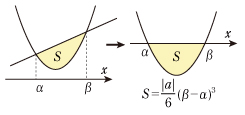
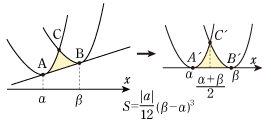
[2] x 軸は特殊な直線なので,直線を y =mx +n として放物線と直線で囲まれる面積を考えてみます。
(2)放物線と接線
[4] 放物線 y =ax2+bx +c と直線(接線)y =mx +n が点 A で接しているとして,A のx 座標をαとします。放物線と接線 y =mx +n と直線 x =β が囲む図形の面積を求めてみましょう。やはり, (ax2+bx +c)−(mx +n) を考えてやれば,接線が x 軸に移り,[3] と同じになりますから,その面積は
[5] 2つの放物線 y =ax2+bx +c ,y =ax2+b'x +c' とその共通接線に囲まれた部分の面積を求めてみましょう。
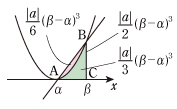
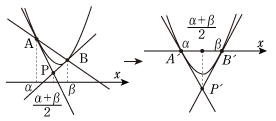
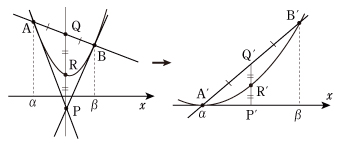
[6] (ア) 放物線 y =ax2+bx +c 上の2点 A(α,*),B(β,*) で接線を引き,2接線の交点を P とおきます。直線 AB を y =mx +n として,またその差 (ax2+bx +c)−(mx +n) を考えます。直線 AB を x 軸に移しているのですから,差の放物線はx 軸とA' (α,0),B' (β,0) で交わります。2点 A,B における接線は,2点 A' ,B' における接線に移ります。放物線の対称性から,この2接線の交点の x 座標は
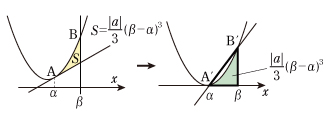
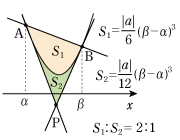
(イ) 放物線と2点 A,B における2接線が囲む図形の面積を求めてみましょう。それは [4] より,
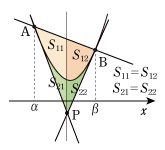
(ウ) 点 P を通る x 軸に垂直な直線は各々の面積をきれいに2等分しています。
(エ) 面積だけでなく,線分にも面白い性質があります。放物線と直線 AB の差ではなく,点 A における接線との差を考えてやれば,この接線が x 軸に移ります。差の放物線はx 軸と点A' (α,0) で接するから y =a (x −α)2 となります。点 P を通る x 軸に垂直な直線は変わらず
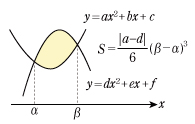
(3)放物線と放物線
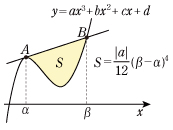
(4)3次関数と接線
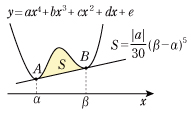
(5)4次関数と接線
(6)発展 |
|
|
3.おわりに
|
|
| 放物線の面積に関することはアルキメデスの頃からわかっていて,いろいろな性質があり楽しめます。2008年の明治大学政治経済学部の入試問題でも楽しく出題されています。2009年の東京工業大学前期の最初の問題も放物線と直交する2つの接線の囲む面積の最小値でした。一昔前の受験テクニックのようですが,曲線の面白い性質を楽しんだ上に,役に立てばと思って上のような事柄に触れることにしています。授業では数学 II で扱うので,(6)の話をしたことはありません。 |