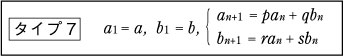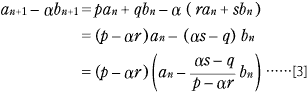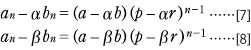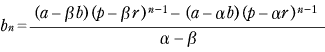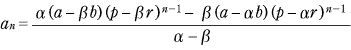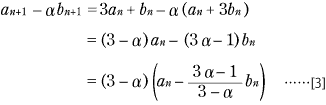| 授業実践記録 | |
| 漸化式の指導について |
|
| 山口県立岩国高等学校 西元教善 |
|
|
はじめに
|
|
| 数学Bで扱う「数列」は生徒の苦手とする分野といえよう。特に,「漸化式」がそうである。
いろいろなパターンがあるように思えて,それを覚えて使うことに四苦八苦している。 入試問題などの漸化式は教科書で扱っている内容を深化させておく必要があるが,本質的なことを押さえておけば十分対応できる。このことを生徒にわかってもらおうと思い,実践(理数科2年次,探究数学)を夏季休暇中に行った。そのときに使ったレジュメから抜粋しながら,実施した内容を紹介する。 |
|
|
レジュメ「漸化式探究」
|
|
| これらは一見すると別物のように見えるが, 逆に, つまり,等差数列と等比数列は見方を変えることで同一視できるのである。 この探究では,一見すると別物に見えるいろいろな漸化式をうまく変形することで,既知の漸化式に帰着させて「漸化式のタイプ」の集約を行って,一般項を求められるようになることをねらいとしている。 次の表は,まとめのページに載せた漸化式のタイプである。
レジュメ(個人的に作成したもの)の構成は,1. an についての1次式型漸化式,2. 分数型漸化式,3. 指数型漸化式,4. 隣接3項間の漸化式,5. 連立型の漸化式であり,1. ではタイプ1〜3,2. ではタイプ4,3. ではタイプ5,4. ではタイプ6,5. ではタイプ7について,それぞれ一般論と具体例で説明した。
連立型の漸化式,つまり,
ここでは an と bn を合体させた数列 例1 [1] −α×[2] から, [4] より,数列 |
|
|
まとめ
|
|
| この実践は夏休みの一日を使っての実践(講義,演習)である。日程は講義 [1] 9:00〜10:15,講義 [2] 10:30〜11:45,昼食,問題演習 [1] 13:00〜14:15,問題演習 [2] 14:30〜15:45である。本校は65分授業を行っているので,1コマをほぼ同時間にとっている。 演習 [1] は生徒一人ひとりが別々の問題を解く時間,演習 [2] は班(1班5人,8班)で大学入試に出題された漸化式の問題を解く時間とした。ともすれば,生徒は見かけが少しでも違えば,違ったものとして認識する。理解ではなく暗記中心の生徒にとっては記憶量に負担をかけ,しかも功を奏しないことが多い。見かけは違っても,元となるもの,考え方,処理が同様であれば,そのことを理解しているだけでも手の打ちようがある。 知らないから「できない,わからない」と諦めるのではなく,知らなくても視点を変えることで「できる,わかる」ことがあることを体験させることも数学教育にとっては重要であると思っている。また,友達と協力して考えることのよさについては,SSH(スーパーサイエンスハイスクール)の実践の中で,多くの生徒の感想に述べられており,今回もそのよさを体験させることにした。効果の程はこれからである・・・ |