| 授業実践記録 | |
| 数学の直感的指導法に関する試み |
|
| 埼玉県立杉戸高等学校 黒野正道 |
|
|
1.はじめに
|
|
|
数学の授業は定義することから始まるが、その定義が抽象的な場合は生徒にとって理解への大きな妨げとなる場合がある。そもそも「定義」とはそう決めることによってうまくいくことが確認されている(well-defined)のであって、そこには具体的・直感的アイディアが存在しているはずである。その一端を(歴史的事実とは異なるかも知れないが)紹介することにより生徒へのより深い理解を促そうというのがねらいである。決して奇をてらったものを考えるのではなく、「説明の順番を入れ替える」や「言葉で表現しやすくする」程度の工夫を念頭に置いている。 |
|
|
2.いくつかの試み
|
|
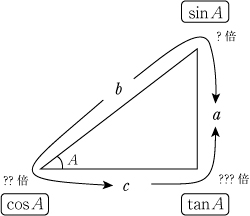
(1)三角比の定義
三角比は一般的には「比」→「倍率」の順序で説明をしていくが、ここでは「倍率」→「比」の順序で説明をしてみた。本来の定義である
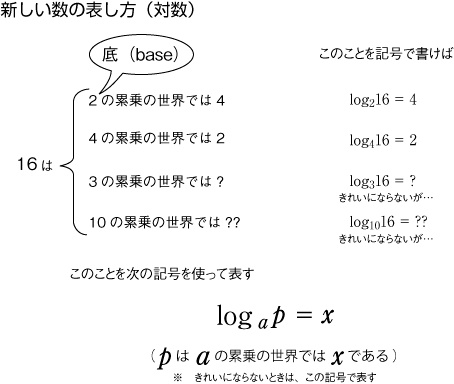
は「三角比の求め方という扱い方」にした。 (2)対数の定義
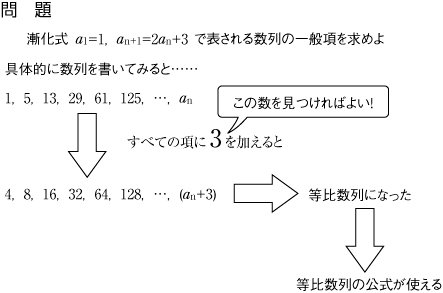
一般的には (3)二項間漸化式の解法
漸化式の問題に対しては解法のテクニックを中心に説明する場合が多くなる。それ故「問題は解けるが、何故このようにやるのかが解らない?」という感想を持つ場合が多いようである。 (4)微分係数
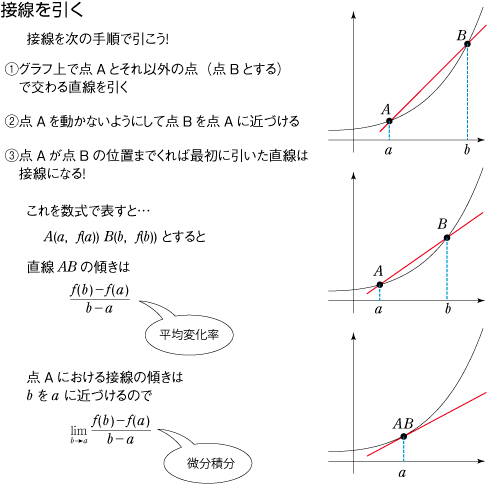
「定義」と「応用」の順序を逆に説明してみた。本来「関数」と「図形」は区別をして話を進める必要があると考える。
と定義をしても「平均変化率」の本質が見えにくいし、ましてやこの極限値である「微分係数」の存在意義など感じられないであろう。 |
|
|
3.おわりに
|
|
|
「理系離れ」「学力低下」が声高に叫ばれる中、一人でも多くの生徒が「数学嫌い」でなくなってくれればと、この20年にわたり微力ながら努力をしてきたつもりである。 |