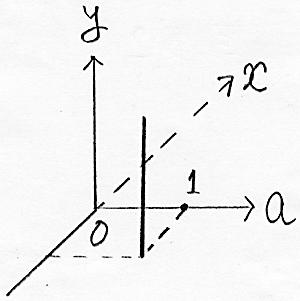いわゆる進学校に勤務して20数年になる。数 I や数 II の単元で、2次関数の応用問題として、関数の最大・最小問題（置き換えをすると2次関数に帰着できる問題）や点の軌跡の問題がある。
　代表的な例としては

問題1．	y = - x2 - 2ax - a +1 のとき、y の最大値の最小値を求める。
問題2．	y = x2+2ax+2a2 - a +1 のとき、y の最小値の最小値を求める。
問題3．	y = (2x)2 - 2x +1 の最小値を求める。
問題4．	y = sin2x - sinx +1 の最大値と最小値を求める。( ただし 0 ≦ x ＜360 )
問題5．	x = - m、y = m2 + m +1 のとき、点( x , y )の軌跡を求めるなどである。

　これらの問題については、生徒は何回か練習することによってだんだん「解ける」ようにはなるが、どの程度「わかっている」かは、疑問であると思われる。
　そこで、より深く「わかる」（ああ、そういうことだったのか！と納得する）ためには、変数が動くイメージを豊かにしたらよいのではないかと考え、後に示すような棒グラフによる立体模型を作って指導してきた。

問題1の解答例としては「最大値をm (a)とすると y = - (x + a)2+ a2 - a +1 となり、x = - a のとき y の最大値 m (a)=a2 - a +1 となる。ここで、この m (a) は a の関数なので、 と変形でき、 のとき、最小値 をとる」と論理的に「解ける」。

　ここでは、生徒の中では、文字 x は変数、文字 a は係数として区別して捉えられているとしよう（ここもずいぶんあやしい生徒が多いと思われるのだが）。
　そこで、 m (a)=a² - a +1 となった後、この文字 a が動く（変わる）ことが、生徒には求められる（つまり係数で固定されていた文字 a が変数となる）。ここで、求めている最大値は与式の頂点の y 座標の値であるが、実際の授業では上記の解答（文字 a による変形）で済まされ、いくつかの a の値を入れたグラフがかかれないままで説明が終わることが多い。たとえグラフがかかれても xy 平面上に a の値を添えてかかれるだけである。このところをもう少し「ていねいに、しかも変数 a によるグラフなども含めて、全体も見えるものにできないか」と思い、次のような棒グラフを用いた立体模型を作り、指導してみた。

〈立体模型の作り方〉
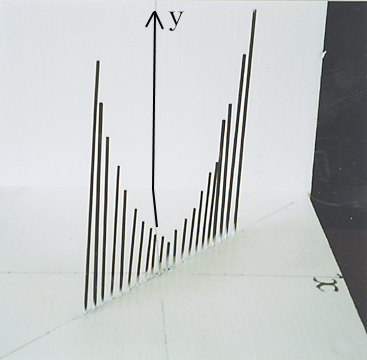
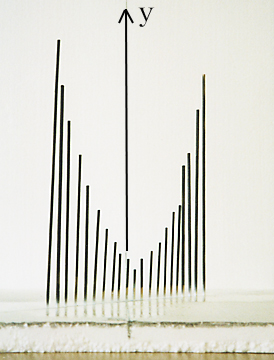
　a =1のときの y の最大値を示す棒を立てる。同様に、いくつかの a の値に対して、y の最大値を示す棒を立てる。　

（ア）立体模型の構成
　　

（イ）xy 平面

（ウ）ay 平面

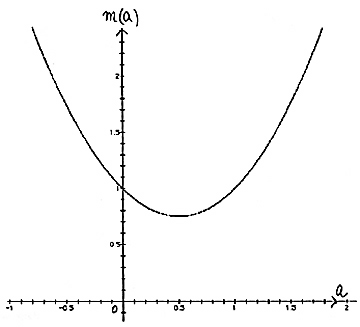
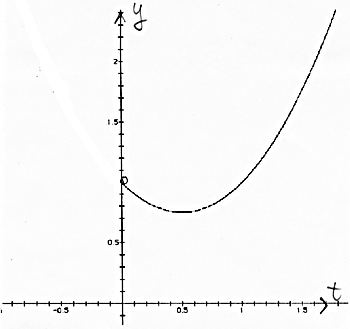
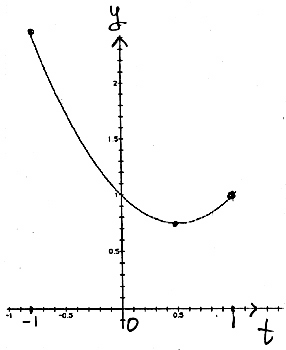
　（ア）を、xy 平面を正面にして見ると（イ）で、a 軸が消えたように見えるグラフである。また、ay 平面を正面にして見ると（ウ）で、これが m (a)=a² - a +1 のグラフになっている。

　問題2は略

　問題3については、数学のアイディアの1つとして「置き換え」があり、それを用いたものである。
　3の解答例としては、 t = 2^x とおくと　t ＞ 0で　 となり のとき y の最小値は 、このとき　 より、x = -1と解ける。

　この2つのグラフをつないで、次のような立体模型で考えてみる。

（ア）全体

（イ）ty 平面

（ウ）xy 平面

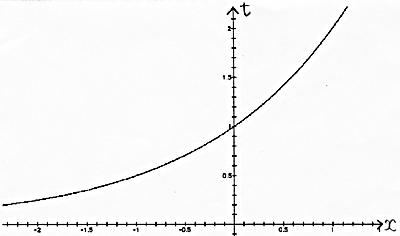
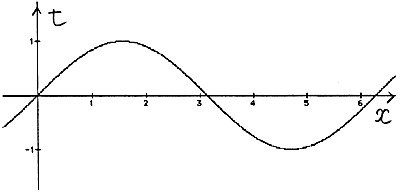
　 t = 2^x は単調増加関数なので、最小となる x の値は1つしかないこともわかる。

　問題4の解答例としては、t = sinx とおくと　0 ≦ x ＜360 より
　-1≦ t ≦1、 となり、-1≦ t ≦1より　 のとき、最小値は 、このとき x =30 、150 。 また、t = -1 のとき最大値は 3 で、x = 270 と解ける。

　これも2つのグラフをつなぎ、立体模型で考えてみると

（ア）全体

（イ）ty 平面

（ウ）xy 平面

　本来は（ウ）の xy 平面から見るべきものを、（イ）の ty 平面から見て解いている。また、t = sinx は周期関数なので、t の値に対して x の値は複数あることもわかる。

　問題5は「図形と方程式」にある点の軌跡の問題である。解法のテクニックとしては「パラメーターの文字を消去」することで解けるのだが、「パラメーターの文字を消去する」とはどんなことかも考えてみる。

　x = - m より m = - x これを y = m²+ m +1 に代入すると、y = x²-x+1

　これで生徒はわかったことになるのだろうか。相当疑問である。生徒たちにわかっているのは、1つの m の値に対して x と y の値が1つずつ定まるということである。

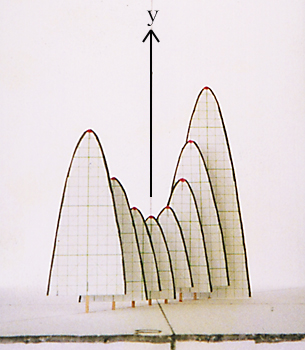
　ここで、m の値を連続して動かしたいとき、棒を多く立てればよく、m と x と y を含めた全体の様子（ア）が、よくわかる。xy 平面を正面から見ると（イ）のグラフになり、この棒グラフがまるで xy 平面に正射影されているように見える。実はこれが「パラメーターの文字を消去」したことになっているのである。

（ア）全体の様子

（イ）xy 平面