|
【生徒への調査】
Q1 高校へ入学したとき,(1年生の4月ごろ)「課題研究」でどの分野をやりたいと思いましたか?(1つだけに○)
a:数学 b:物理 c:化学 d:生物
|
a |
b |
c |
d |
| 1年 |
5 |
2 |
18 |
14 |
| 2年 |
1 |
10 |
10 |
13 |
| 3年 |
1 |
10 |
12 |
14 |
Q2 2年以上の生徒へ質問します。実際の課題研究は何を選びましたか?
a:数学 b:物理 c:化学 d:生物
|
a |
b |
c |
d |
| 2年 |
2 |
13 |
9 |
11 |
| 3年 |
3 |
12 |
11 |
11 |
Q1とQ2より課題研究の科目の移り変わりは,次のとおりである。
|
数→数 |
数→理 |
理→数 |
| 2年 |
0 |
1 |
2 |
| 3年 |
0 |
1 |
3 |
Q3 数学の課題研究に魅力を感じますか?
a:大いに感じる b:少し感じる c:あまり感じない d:全く感じない
|
a |
b |
c |
d |
| 1年 |
4 |
21 |
8 |
3 |
| 2年 |
6 |
11 |
15 |
3 |
| 3年 |
4 |
11 |
14 |
13 |
Q4 もし,「課題研究」で数学をするとすれば,どのようなことをやってみたいですか?
a:具体的なものがある。(具体的に書いて下さい)
b:今は具体的なものが浮かばないが,時間をかければ見つかりそうである。
c:時間をかけても何をしてよいか,見つかりそうにない。
|
a |
b |
c |
| 1年 |
4 |
25 |
8 |
| 2年 |
7 |
20 |
8 |
| 3年 |
6 |
19 |
12 |
a の具体的なものは,次のとおりである。
1年
|
○難しい公式を証明してみる ○サイコロを何回も振って出る目の確率をもとめる,○円周率の3.14以降の数をでるところまで計算する ○数列
|
2年
|
○数列を他の分野に応用させる ○sinθのグラフ ○ピタゴラスの定理の応用,○昔の人がどのようにして数学を生み出したか ○フェルマーの最終定理の証明
|
3年
|
○平面幾何について何か ○学校で習ったことを図形的に考察,○微分積分 ○長い式 ○宝くじの確率 ○連動表 ○二項定理について
|
【教員への調査】
Q1 課題研究をするとしたら,どのような研究をされますか。
|
○ラグビ-ボ-ルの体積を求める ○マンホールの蓋はなぜ丸いか ○連分数 ○和算 ○コンピュータ等で実験をして,法則等を見つけ証明させる ○三平方の定理の証明,○高校生の力で考えてできる内容(教師の力量のコンテストではないもの) ○アジアの数学(九章算術や和算から見る数学) ○連続とはどういう意味か,ε-δ論法をアルキメデスとカメに例えて,そこから 0.9999…=1 の証明および実数とは何かを探る ○方程式とは,文字とは何かをヴィエタなどの数学者を追いながら文字の役割をもう一度見直す ○様々な面積を調べながら積分の基礎を発見する
|
Q2 課題研究を通して苦労された点と楽しかった点をお書き下さい。
|
○ |
2年の初旬では学習内容が少ないこと。そのために,微積などの説明に時間を費やした。また,生徒と共に考えるところがよい。
|
|
○ |
テーマを決めるのに,身の回りのことや授業で学習した内容がテーマとなりにくいので苦労した。
|
|
○ |
生徒に定理などの証明をさせることに苦労した。また,参考文献を調べていくうちに新しい発見があたっとき楽しかった。
|
Q3 数学の課題研究を通して,教員や生徒が得たものをお書き下さい。
|
○ |
生徒にとって「高校数学は教えられるもの」というイメージが強いが,「数学は自ら考えるもの」ということが伝えられてよかったと思う。
|
|
○ |
新しい発見をしていく喜びや数学的に論証していく力がつくこと。
|
|
○ |
著作権についての知識が身に付いたこと。
|
|
○ |
コンピュータ(ワードの数式エディタ,パワーポイント)の習熟ができ,プレゼンテーション能力が身に付いたこと。
|
<本校の具体的研究例>
sin1°への挑戦
1 研究動機
三角比は数学の中でよく使う機会があり,「どんな人がこんなことを考えたのか?」「なぜ,それが必要だったのか?」「どのようにして sin1°の値を,求めたのか?」などということに疑問を感じていました。だから,疑問を解明するために三角比について調べ,sin1°を自分たちで求めるために,この研究を行いました。
2 三角比の起源について
三角比の起源については,「話題源数学」(とうほう出版)に次のように記載されていました。
「三角法は英語で trigonometry であるが,この語源は trigonon(三角)+metria(測る)で,三角測量である。三角法は最初ギリシアの天文学において,天体の距離の測量に利用するための弦の表として生まれたものである。有名なギリシャの天文学者プトレマイオス(紀元150頃,英語読みトレミー)の『アルマゲスト』には半径60の円の中心角 (AOB)0.5°ごとの弦ABの表とその計算法が書かれている。AB をcrdα で表すと,crdα=120sin 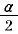 の表である。 の表である。
ギリシアの天文学とともに,弦の表はインドへ伝わった。ギリシアの弦の表は,∠AOB に対する AB の長さを示す全弦の表であったが,インド人はこれを 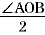 に対する に対する  AB=AM の半弦の表に改良した。インドのアリアバタは,半径を3438とし,3 AB=AM の半弦の表に改良した。インドのアリアバタは,半径を3438とし,3 45'ごとの半弦の表を作っている。3 45'ごとの半弦の表を作っている。3 45' は,90 45' は,90 を24等分したものであるが,これは正96角形は円と見なしうる考えに基づいている。3438というのは,円を 360 を24等分したものであるが,これは正96角形は円と見なしうる考えに基づいている。3438というのは,円を 360 に分け,これをさらに360×60=21600分に細分し円周率を 3.1416 とし,2πr =21600から算出したものである。」 に分け,これをさらに360×60=21600分に細分し円周率を 3.1416 とし,2πr =21600から算出したものである。」
3 sin 1°について
僕たちは,三角比の表の sin1 というのが気になりました。昔の数学者はどのようにしてその値を求めたのでしょうか?僕らが予測した方法は,まず直角を作図し,それを90等分した後,糸で長さを測り値を求めるというものです。しかしこの方法では,直角が精密でなく,それに糸の伸び縮みを無視できない等の問題がでてきます。だから,計算で求めたのではなかろうか,と考え実証することにしました。 というのが気になりました。昔の数学者はどのようにしてその値を求めたのでしょうか?僕らが予測した方法は,まず直角を作図し,それを90等分した後,糸で長さを測り値を求めるというものです。しかしこの方法では,直角が精密でなく,それに糸の伸び縮みを無視できない等の問題がでてきます。だから,計算で求めたのではなかろうか,と考え実証することにしました。
まず加法定理で sin15 を次のようにして求めました。 を次のようにして求めました。
sin15 =sin (45 =sin (45 -30 -30 ) = sin45 ) = sin45 cos30 cos30 - cos45 - cos45 sin30 sin30
= 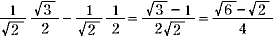 また cos15 また cos15 = = 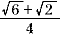
次に θ=18 とおくと cos2θ=sin3θ が成り立つので とおくと cos2θ=sin3θ が成り立つので
cos2θ=1-2sin2θ,sin3θ=3sinθ-4sin3θ より
1-2sin2θ=3sinθ-4sin3θ sinθ=x (0< x <1) とおくと
4x3-2x2-3x+1=0 (x-1)(4x2+2x -1)=0
0< x <1 より x= 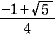 よって,sin18 よって,sin18 = = 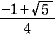 また cos18 また cos18 = = 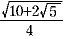
さらに加法定理でsin3 を計算すると を計算すると
sin3°=sin(18 -15 -15 )=sin18 )=sin18 cos15 cos15 -cos18 -cos18 sin15 sin15
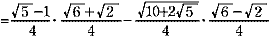
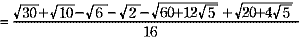
ここで sin3 =3sin1 =3sin1 -4sin31 -4sin31 よりsin1 よりsin1 =x とおき整理すると =x とおき整理すると
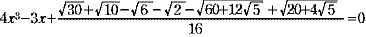
この方程式は2次の項のない3次方程式なので,まず特別な3次方程式の解の公式を使って解くことにしました。しかし,3時間以上も費やして計算しましたが,結局自分達の力で解けませんでした。
そこで,僕らは上式の左辺を f(x)とおき増減表を求めました。
|
x |
-1 |
…… |
-0.5 |
……
|
0.5
|
……
|
1
|
| f ' (x) |
|
+ |
0 |
- |
0 |
+ |
|
| f (x) |
負
|
 |
正
|
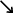 |
負
|
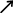 |
正
|
このことで,-1< x <1の区間に異なる実数解を3つ持つことがわかりました。
また,グラフはつぎのようになります。
これでは,sin1 の値が3つあることになります。当然,原点に最も近い x 軸との交点が sin1 の値が3つあることになります。当然,原点に最も近い x 軸との交点が sin1 の値です。それでは他の2つの交点は何なのでしょうか?僕らは sin3 の値です。それでは他の2つの交点は何なのでしょうか?僕らは sin3 の3 の3 に着目し,一般角を考えました。sin3 に着目し,一般角を考えました。sin3 =sin(3 =sin(3 +360 +360 ×k) (k は整数) より,交点は左から sin (1 ×k) (k は整数) より,交点は左から sin (1 +120 +120 ×k) に k=-1 , 0 , 1を代入した値,即ち sin (-119 ×k) に k=-1 , 0 , 1を代入した値,即ち sin (-119 ) ,sin1 ) ,sin1 ,sin121 ,sin121 です。 です。
次に,「Mathematica」という数学ソフトを使って3次方程式を解きました。
この方程式の1つの解は,x= 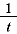 である。ただし, である。ただし,
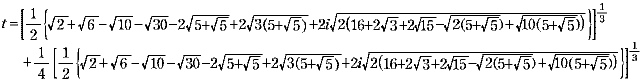
また,他の解は 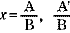 である。ただし, である。ただし,
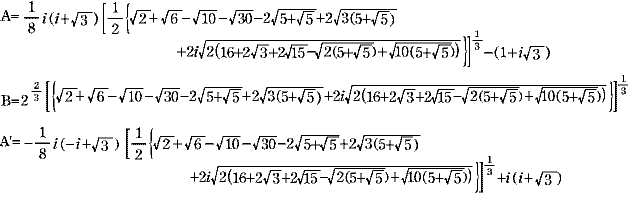
これでは,すべて虚数解になりそうですが,解をまとめていけば実数になると思われます。
4 まとめ
僕らは結局,計算だけで, sin1 の値を求めれませんでした。それでは,最初の疑問である『昔の人はどのようにして sin1 の値を求めれませんでした。それでは,最初の疑問である『昔の人はどのようにして sin1 を求めたのか』ということですが,おそらく何百時間もかけて計算したか,あるいは非常に精度が高い近似値の計算方法を知っていたのではないか,と僕らは考えました。 を求めたのか』ということですが,おそらく何百時間もかけて計算したか,あるいは非常に精度が高い近似値の計算方法を知っていたのではないか,と僕らは考えました。
僕らも,Mathematica を使う前に近似値計算をしたところ,真の値と 0.003 もずれていて,これを角度にすると 619分になります。
最後に,僕らが何時間も考え解けなかった方程式を,コンピュ-タはほんの数秒で解いてしまった
ことに驚くとともに,いつかは自力で解きたいと思いました。
参考文献:「話題源数学」(とうほう出版)
|