| 授業実践記録 | |
| グラフの性質を探る −評価方法と絡めて− |
|
| 埼玉県立日高養護学校 青木猛正 |
| ※ 下記は,総合学科高等学校である筑波大学附属坂戸高等学校および埼玉県立戸田翔陽高等学校で行った実践記録である. |
|
|
1. はじめに
|
|
| 通常,「数学 I 」における2次関数の一般形のグラフをかく際には,中学校の既習事項である「2乗に比例する関数」として,頂点が原点にある2次関数のグラフを用いている.そのグラフを y 軸方向の平行移動と x 軸方向の平行移動をそれぞれ指導した後に,それらを組み合わせて頂点の平行移動を捉えている.その後に,一般形の2次関数の平方完成を扱っている. しかし,y=ax2 から,y=ax2+q,さらに y=a (x−p)2 への流れには,いささか違和感を感じている.平行移動の必然性が十分に生徒には伝わらず,唐突な感は否めない. また,上記の展開の際においても,まず対応表を作成し,その結果を座標平面にプロットしてグラフを作成している. そこで,対応表をもとにしてグラフをかくことを通して,2次関数の持つ諸性質を捉えることによって,数学的な見方や考え方を生徒自らが獲得でき,自らの発想を自己評価できるような事例を挙げてみる. |
|
|
2. 準備
|
|
| そもそも「関数」の概念をどのように認識させるかが重要である.生徒に「関数とは?」との発問をすると,多くの答えは「グラフ」である. そこで,筆者は2次関数の導入として, 関数とは,自動販売機である との表現でイメージ付けを行っている.これは,従来の「ブラックボックス」の発想を現代的にアレンジしたものである. |
|
|
3. 展開1
|
|
|
関数のイメージを捉えたところで,生徒にはワークシートを配付して,まず次の課題を与えて具体的な数関数を捉えさせている. 課題1 次の x と y の関係を式で表してみよう. これらの式を求めることにより,2乗に比例する関数ばかりではなく,一般の二次関数の存在を意識させることができる.すなわち,y=ax2+bx+c の形で表せる「関数」の存在について実感を持たせることができる. |
|
|
4. 展開2
|
|
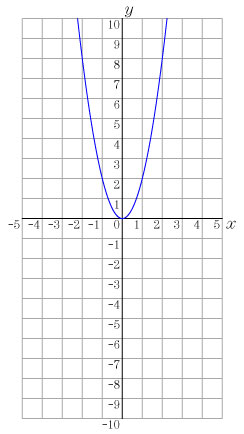
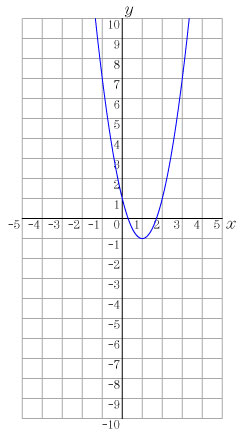
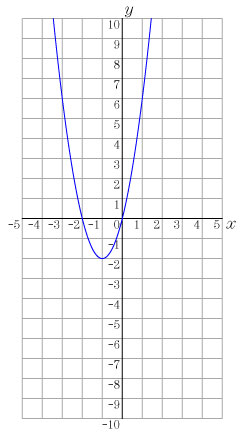
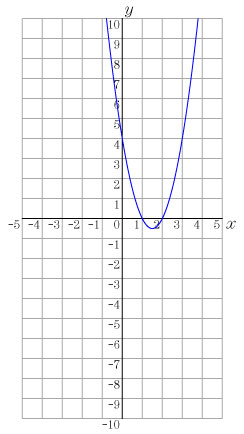
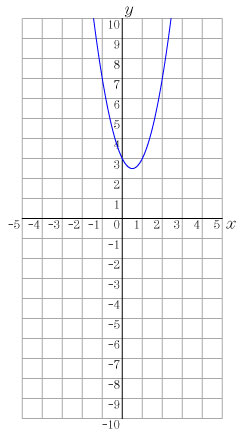
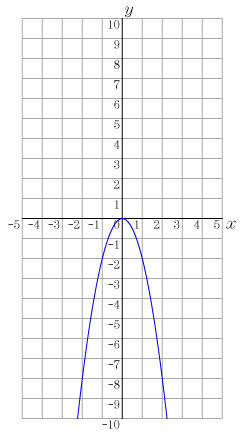
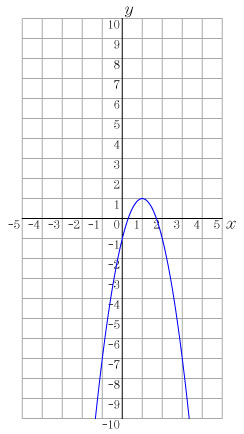
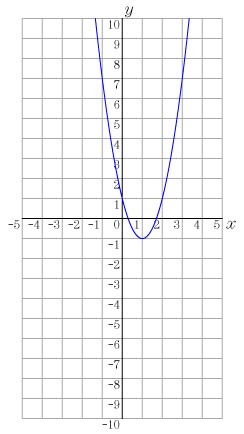
課題2 y=2x2 のグラフを描いてみよう. この発問は,純粋に中学校の復習として扱うことができる.この際に,大きめの方眼紙(B4サイズ程度)を与えてグラフをかかせる. 課題3 次の式に対し,対応表を作成し,その点を課題2のグラフをかいた座標平面に点を打って,グラフをかいてみよう.
生徒は,対応表を作って点をプロットする作業は比較的好んで行う.授業では,手計算で対応表を作らせたが,電卓やパソコン等の活用も考えられる.また,班を構成して,その班で分担することも考えられる.ただし,グラフ電卓やグラフ作成ソフトの活用は,望ましくはない.あくまで,点をプロットしてグラフの概形を作成させることに意義がある.
|
|
|
5. 展開3
|
|
|
課題4 今かいたグラフをよく見て,そこから分かることを書いてみよう. 上記の課題を通して,生徒自身によるさまざまな発想を生かすことにより,主体的な学習態度の育成を図ることができる. そのために,まず生徒がかいたグラフ(黒板や OHP 等で確認をする)を見ながら,生徒自身が感じたことや確認できる点等どのようなことでもまとめさせる習慣をつけることは意味を持つ. 生徒には,どのようなことでもいいから書き出してみるように指導する. 課題5 課題4 で書いたことを発表しよう. 課題6 人の発表を聞いた結果から,自分の書いたことについて評価してみよう.
各課題では,単に問題解決だけを目的とせず「・・・について評価してみよう」のように,課題解決の経過や結果を自己評価させるように試みた.これは,単に演習の結果をノートに○や×をつけて済ますのではなく,自分の解答と他者の解答との比較によって,課題の内容がより深まることをめざした. |
|
|
6. 評価の方法
|
|
|
数学科における評価の観点としては,「関心・意欲・態度」「数学的な見方や考え方」「表現・処理」「知識・理解」の4項目が挙げられている.
従来から,「評価」というと「知識・理解」のイメージが強い.特に高等学校においては,中学校のように観点別評価が前面に出されていないため,「関心・意欲・態度」の扱いについては課題となっている.
今回の展開については,下記の「評価の規準」を設けた
特に,上記の課題4〜課題6を設けたことは「関心・意欲・態度」や「数学的な見方や考え方」の評価資料とすることを想定している.この取り組みに関しては,随時ワークシートを回収し,学習に対する態度や自らの学習の振り返り,学習事項のまとめ等をもとに,関心・意欲・態度や数学的な見方や考え方の観点からの評価を行った. |
|
|
7. 評価に関する考察
|
|
|
(1) 新しい評価観
「評価」に対する現場教師のイメージは,生徒の学習成果を数量的に表すことを主眼とした,「評定」としての捉え方からまだまだ抜けきらないのが現状であると言える.極端に言えば,「評価」=「テストの点数」との認識が実態である. このことは,学習指導において共通の到達度目標を設定し,すべての生徒に共通の尺度を設けた評価活動と言える.しかし,この評価はあくまで教師サイドから見た生徒に対する評価であり,達成目標に基づくものである.その結果,学力を断片的な知識の蓄積と捉えるのみになり,「知識・理解」や「表現・処理」の認知的領域等の「実体的な学力」すなわち「内容知」のみがクローズアップされることになってしまった.そこから,「学力問題」が揶揄されているのが現状である. しかし,新しい学力観や[生きる力]に応じた新しい評価観としては,生徒の学ぶ過程や学ぶ意欲,学んだ成果の総合化が求められることになる.すなわち,知識の蓄積だけではなく,知識の活用といった「機能的な学力観」に基づいて,「関心・意欲・態度」や「数学的な見方や考え方」等の「方法知」や情意領域がよりクローズアップされなければならない.この「方法知」はむしろ評価の観点の中心に据える必要さえある. そのためには,評価活動自体が日々の学習活動の中で行われなければならないし,評価の結果がその後の学習や指導に反映するものでなければならない.すなわち,生徒の内面的な意識である主観部分を十分な客観性を持って評価することである.従来のように知識量や技能の獲得状況のみで判断はできない分,すべての生徒に対して必ずしも共通な尺度を持ちうるものではない. (注)「機能的な学力」と「実体的な学力」に関しては,安彦1996を参照
(2) 3つの目標類型
従来は,「達成目標」が重視されていたと言える.その結果,高校生の「体験不足」が指摘されている.学習の目的が「テストのため」や「入試のため」となり,既習事項の暗記に終始し,学習内容が実感として生徒の心の琴線に響くことが少ない.また,学習成果の縦方向への系統性は持ち得ても,横方向への広がりが欠けている.その結果,実社会における数学の有用性が理解されず,「感動」を経験することもできないでいる.そのため,学習した内容を真の意味の「力」として実感できる機会も乏しい.
(3) 3つの目標類型の構造
(4) 数学的活動と目標設定の関連
の3点を例示している.
となりうると考える.
(5) 数学における目標類型と評価の観点の関連
ただし,この3つの目標類型と評価の観点については,上記のように完全に区分けをするという意味ではなく,それぞれの目標においても様々な観点から評価する必要がある.
引用文献・参考文献 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||