| 授業実践記録 | |
| 垂心の存在証明 |
|
| 福岡県立小倉高等学校 繁木伸孝 |
|
|
1.はじめに
|
|
| 平成15年度からの新教育課程では,数学Aに平面幾何が登場している。本年,1年生を担当し,この単元の指導を行った。はじめての経験であったので,教材選択や指導法など随分勉強になったと思う。その中で特に印象深かった垂心の存在証明についてまとめてみる。 なお,本校で使用している教科書における指導内容の概略は次の通り。 §1 三角形 【1°重心,外心,内心 2°三角形の辺と角】 §2 円 【1°円周角定理 2°方べきの定理 3°2つの円】 |
|
|
2.問題設定
|
|
| 本章の第1時限目の授業では,§1の重心,外心,内心として1つずつの“心”を定義し,主な性質を1,2つ解説した。例えば, 定義:△ABCの各辺の垂直二等分線は1点で交わる。その点Oを外心と呼ぶ。 性質:外心を中心として,3頂点A,B,Cを通る円(外接円)を描くことができる。 と板書し,図を描いた。 重心G→外心O→内心 I と同じ形式,リズムで解説を進めたが,次時に設定した練習問題の中に,垂心Hも含むものを予定していたので教科書にはないが, 定義:△ABCの角頂点から対辺に下ろした3つの垂線は1点で交わる。その点Hを垂心と呼ぶ。 と板書し,図を描いた。 ところで,この定義については,“垂心”なる用語の設定であり,下線部分の3直線が“1点で交わる”ことは定理である。重心,外心,内心では,この“1点で交わる”ことを教科書通り,簡単な証明を与えつつ授業を展開した。ただ,“垂心”での“1点で交わる”ことについては, 「今は証明はヒミツ。自分でできた者は証明を提出せよ。正解者には賞品を出す。」と結び,ちょうど授業のチャイムが鳴るという授業であった。
|
|
|
3.証明作成
|
|
翌朝,早速,意欲的な生徒が次のような証明を作成してきた。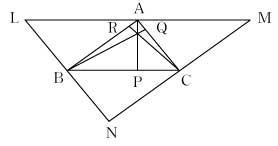 [証明1]
[証明1]Aを通り辺BCに平行な直線,Bを通り辺ACに平行な直線,Cを通り辺ABに平行な直線を描き,図のように△LMNを定める。また,3本の垂線の足をP,Q,Rとする。△ABC≡△BAL≡△CAMであるから,LA=MAとなり,AはLMの中点。さらに,BC//LMなのでAPはLMの垂直二等分線である。同様に考えると,3本の垂線の交点は△LMNの外心であり,確かに1点に定まる。
L,M,Nの設定など難しい証明だと感じていたので反応が不安であったが,見事に期待に応えてくれた生徒がいた。次時のはじめでクラスに紹介し,皆の前で賞品(数学の本)をプレゼントし,正解者を大いに褒めた。
この問題が証明できれば,∠ARH=90°となり,点Hが垂心として存在することになる。教科書でもこの例題の証明の後,補足として「垂心」について触れている。この証明の存在に気付き,証明を写して提出する生徒が出たら賞品はどうしようかとも思ったが,期待していた正解を自身の力で得た生徒が出て,出題した私も大変うれしかった。
この例題はかなり難しい証明問題だと思うが,[証明1]の話題が記憶に残っていたせいか,生徒の反応が思ったより良かった気がした。 |
|
|
4.比較検討
|
|
| 他社の教科書で問題をどのように取り扱っているか調べてみた。生徒の考えた[証明1]の方針で,例題や誘導形式の章末問題になっているもの,また,チェバ,メネラウスの定理の指導項目が設定されており,その応用として章末問題で取り扱われているものなどがある。
したがって, 同様にして,
したがって,
よって,チェバの定理の逆よりAP,BQ,CRは1点で交わることが示された。
本校ではチェバ,メネラウスはこの単元では指導しないことにしている。それは,ベクトルの単元で,例の一次独立の問題に対し,裏技に終始させないためでもある。
[証明1]から[証明3]までを振り返ると,それぞれ特徴があって興味深い。 |
|
|
5.最後に
|
|
| 平面幾何を指導する際,授業では次の3点について特に留意したつもりである。 [1] 図はなるべく大きくていねいに描く。また図形の彩色についても特に配慮する。 [2] 説明のとき指示代名詞(「その点が」「あの三角形を」など)を用いず,具体的な指示(「赤い線分」「黄色の点」「斜線を付けた三角形」など)を心掛ける。 [3] 着眼点と証明作成のストーリー立てを重視し,証明完成の Key となる事項(利用した定理や上手な補助線など)が明らかになるように解説する。 平面幾何の指導の状況は実際どうなのであろうか。色々な工夫が具体的になされているだろう。正直に言って,まだまだ問題解決や指導に自信の持てない分野である。教材研究のポイントや教授法について,ご意見やアドバイスをご教示いただければと願っている。 Eメール::YHW02304@nifty.ne.jp |
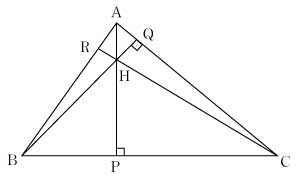 例題
例題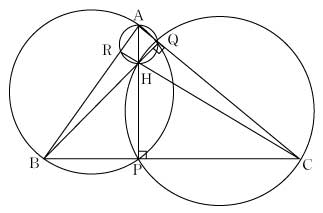 [証明2]
[証明2]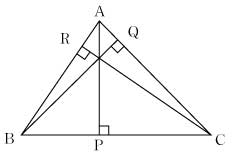 [証明3]
[証明3]