| 妛廗妶摦 |
妛廗撪梕 |
巜摫忋偺棷堄揰 |
| |
侾丂慜帪偺妛廗偺妋擣 |
 |
|
|
| |
乻慜帪偺壽戣乼
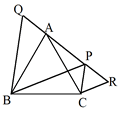
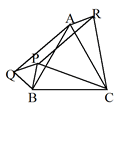
丂惓嶰妏宍俙俛俠偺撪懁偵揰俹傪偲傝丆俛俹丆俠俹傪偦傟偧傟侾曈偲偡傞惓嶰妏宍俻俛俹丆俼俹俠傪丆仮俹俛俠偺奜懁偵偮偔傝傑偡丅
丂偙偺偲偒巐妏宍俙俻俹俼偼偳傫側巐妏宍偵側傝傑偡偐丅 |
 |
暯峴巐曈宍偵側傞
乻棟桼乼崌摨側嶰妏宍
乣懳墳偡傞曈
乣俀慻偺懳曈偑摍偟偄 |
|
|
| |
|
|
|
| 丒 |
揰俹偑惓嶰妏宍ABC撪偺偳偺埵抲偱傕惉傝棫偮偙偲傪偍偝偊傞丅 |
| 丒 |
徹柧婰弎偲恾傪徠崌偟妋擣偡傞丅 |
|
|
| |
俀丂忦審曄偊乮敪揥乯偺峫嶡 |
|
|
| |
| 乮侾乯 |
壽戣採帵乽俹傪惓嶰妏宍ABC偺奜偵偡傞偲偳偆偐乿 |
|
|
|
| |
乻杮帪偺壽戣乼
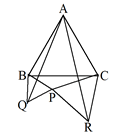
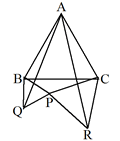
丂惓嶰妏宍俙俛俠偺奜懁偵揰俹傪偲傝丆俛俹丆俠俹傪偦傟偧傟侾曈偲偡傞惓嶰妏宍俻俛俹丆俼俹俠傪丆仮俹俛俠偺奜懁偵偮偔傝傑偡丅
丂偙偺偲偒傕丆慜帪偺寢榑乽巐妏宍俙俻俹俼偼暯峴巐妏宍乿偼曐徹偝傟偰偄傞偱偟傚偆偐丅 |
|
|
| |
|
|
| 丒 |
嶌恾僣乕儖偱揰偑摦偔條巕傪墘帵偡傞丅惗搆傪巜柤偟偰憖嶌偝偣偰傕傛偄丅 |
|
|
| |
|
|
|
| |
|
|
|
| |
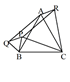
| 恾俬 |
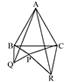
恾俬俬 |
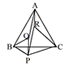
恾俬俬俬 |
恾俬倁 |
 |
 |
 |
 |
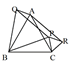
| (AC偺塃懁) |
(AB偺嵍懁) |
(BC偺壓懁) |
(BC偺壓懁) |
恾俬俬俬偼墯巐妏宍
恾俬丆俬俬丆俬倁偱偼暯峴巐曈宍偵側偭偰偄傞傛偆偩丅 |
|
惓嶰妏宍傪
奜懁仺忋懁 |
|
|
| 丒 |
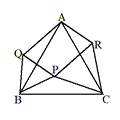
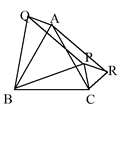
惓嶰妏宍ABC偑偐偐傟偰偄傞儚乕僋僔乕僩偵揰俹傪偐偒崬傒丆恾俬丆恾俬俬丆恾俬俬俬側偳傪嶌惉偝偣丆仮PBC丆仮RAC丆仮QAB偑崌摨偵側傝偦偆側偙偲傗丆暯峴巐曈宍偵側偭偰偄傞條巕傪妋擣偡傞丅偙偙偱偼徹柧婛弎偵偼偙偩傢傜偢丆捈娤揑偵妋擣偱偒傟偽傛偄丅 |
|
|
| |
| 丒 |
崻嫆傪帩偪側偑傜嬝摴棫偰偰妋偐傔傞 |
| |
崌摨側嶰妏宍乣懳墳偡傞曈乣惓嶰妏宍偺曈乣俀慻懳曈偑摍偟偄 |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
乽側偤揰俹傪摦偐偟偰傕暯峴巐曈宍偵側傞偺偐乿 |
|
| 丒 |
仮PBC偺奺曈傪侾曈偲偡傞乽惓嶰妏宍乿偱偁傞偙偲丆惓嶰妏宍偺惈幙偵埶嫆偟偰偄傞偙偲傪慡懱偱妋擣偡傞丅 |
|
|
| |
|
|
|
| |
| 仢 |
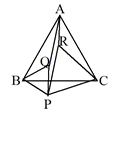
乽俀曈乿偼慜帪徹柧偲摨偠丆乽娫偺妏乿傪妋擣 |
| |
| 恾俬丂 |
佢PCB=佢RCA=60亱+佢ACP |
| 恾俬俬丂 |
佢PCB=佢RCA=60亱-佢ACP |
|
|
|
| 丒 |
娫偺妏偑摍偟偄棟桼傪惗搆偳偆偟偱愢柧偟揱偊崌傢偣傞丅 |
|
|
| |
|
|
|
|
| |
| 乮係乯 |
仮ABC,QBP,RPC偑惓嶰妏宍偱側偐偭偨傜偳偆側傞偐傪恾帵偟偰妋擣偡傞 |
|
|
| 丒 |
擇摍曈嶰妏宍丆惓曽宍側偳偱傕惉傝棫偮丅乽摍偟偄曈乿傗乽摍偟偄妏乿傪崻嫆偵愢柧偑偮偔偙偲傪妋擣偡傞丅 |
|
|
| |
 丂丂丂 丂丂丂 |
|
|
| |
| 乮俆乯 |
巐妏宍AQPR偑摿暿側宍偵側傞偺偼丆俹偑偳傫側埵抲偺偲偒偐傪媍榑偡傞 |
|
| 丒 |
挿曽宍乮佢BAP=150亱乯 |
| 丒 |
傂偟宍乮PA=PB乯 |
| 丒 |
惓曽宍乮挿曽宍偐偮傂偟宍乯 |
|
|
   |
|
| |
|
|
|
|
|
| |
俁丂傑偲傔偲丆偝傜側傞忦審曄偊乮敪揥乯偺帵嵈 |
|
|
|
| |
| 丒 |
徹柧偼丆摨偠忦審偺慡偰偺恾傪戙昞偟偰偄傞丅乮徹柧偺堦斒惈乯
|
| 丒 |
挿曽宍丆傂偟宍丆惓曽宍偼丆暯峴巐曈宍偺堦庬偲尒傞偙偲偑偱偒傞丅 |
|
|
|
|
| |
|
|
|
|
|






 丂丂丂
丂丂丂