| (1) | 線分の図
線分の図で,1つ1つの線分を辺,その両端の点を頂点ということにする。
頂点の数をv, 辺の数をeとする。
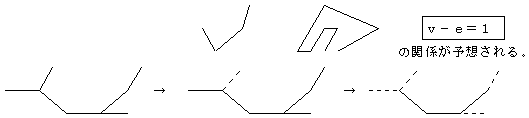
1つの樹形があったとき,これから,端の枝にある線分を1つとった樹形をつくる。すると,vもeも1つずつ減るからv−eの値は変わらない。枝にある線分をとる操作を,さらに続けていっても,v−eの値は,やはり変わらない。そして,最後に,1つの線分となり,このとき,v−e=1だから,もとの図についてもv−e=1となる。
|
(2) |
線分と面の図
線分の図に,それがかこむ面を含めて考えることにする。
頂点の数をv,辺の数をe,面の数をfとする。
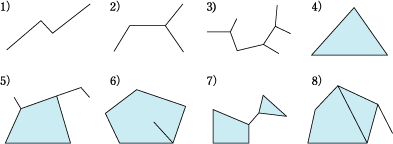
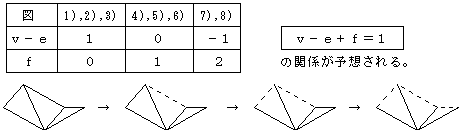
図のように外側の辺を1つ取り外し(頂点は残す),これを辺に持つ面も同時に取り除くと,頂点の数は変わらず,辺の数は1つ減り,面の数は1つ減るから,v−e+fの値は変わらない。この操作を繰り返し行っていっても,その途中での,v−e+fの値は変わらない。そして,図形はついには,樹形(閉曲線を1つも含まない線分の図)になって,そのとき,v−e=1,f=0となる。だから,v−e+f=1である。したがって,もとの図についてもv−e+f=1となる。 |
(3) |
オイラーの定理
多面体の頂点の数をv,辺の数をe,面の数をfとする。
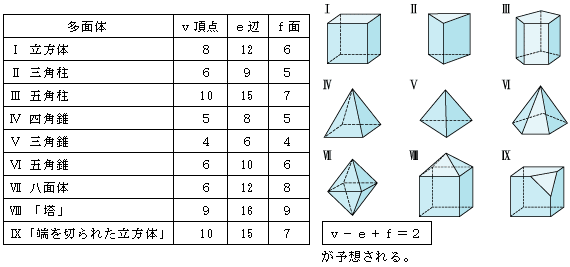
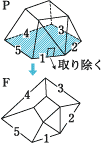 1つの多面体Pで,頂点の数をv,辺の数をe,面の数をfとする。
1つの多面体Pで,頂点の数をv,辺の数をe,面の数をfとする。
多面体Pから,1つの面を取り除く。できた穴を広げて,残りの面全体を,つながり具合を変えずに,平面上の線分と面との図Fにする。
この図Fにおいては,頂点の数はv,辺の数はe,面の数はf−1であるから,
v−e+(f−1)=1
したがって,多面体Pの頂点,辺,面,v,e,fについて,次の関係が成り立つ。
| オイラーの定理: |
多面体で,頂点の数をv,辺の数をe,面の数をfとすると,
v−e+f=2 |
|
|
|
(4) |
正多面体の辺の数
多面体では,どの辺も隣り合う2つの面(多角形)の辺になっているので,正多面体では,(辺の数)=(1つの面の辺の数)×(面の数)÷2の関係が成り立つ。
|
(5) |
発展
| ・ | 右図のような線分と面の図で,頂点の数をv,辺の数をe,面の数をfとする。v,eは変わらず,穴が1つ空いているとf−1,2つ空いているとf−2となるので,
ア)v−e+f=0 イ)v−e+f=−1
一般に穴が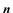 個空いているとすると,v−e+(f− 個空いているとすると,v−e+(f−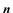 )=1− )=1−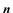 となる。 となる。 |
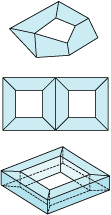
| ・ | 図のような立体の表面で,頂点の数をv,辺の数をe,面の数をfとする。v,eは変わらず,穴が1つ空いているので,面の数は立体なので2つ減り,f−2となるのでv−e+f=0
一般に穴が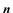 個空いているとすると,v−e+(f−2 個空いているとすると,v−e+(f−2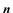 )=2−2 )=2−2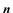 となる。 となる。 |
|
 |
|





